
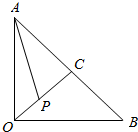
 如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.
如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$. 分析 如图所示,$\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}$,设$|\overrightarrow{OP}|$=t≥0.可得$\overrightarrow{AP}$•$\overrightarrow{OP}$=$(\overrightarrow{OP}-\overrightarrow{OA})$•$\overrightarrow{OP}$=t2-$\frac{\sqrt{2}}{2}$t=$(t-\frac{\sqrt{2}}{4})^{2}$-$\frac{1}{8}$,利用二次函数的单调性即可得出.
解答 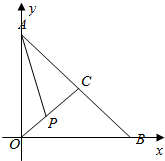 解:如图所示,$\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}$,
解:如图所示,$\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}$,
设$|\overrightarrow{OP}|$=t≥0.
∴$\overrightarrow{AP}$•$\overrightarrow{OP}$=$(\overrightarrow{OP}-\overrightarrow{OA})$•$\overrightarrow{OP}$
=${\overrightarrow{OP}}^{2}$-$\overrightarrow{OA}•\overrightarrow{OP}$
=t2-$\frac{\sqrt{2}}{2}$t
=$(t-\frac{\sqrt{2}}{4})^{2}$-$\frac{1}{8}$
$≥-\frac{1}{8}$.
当t=$\frac{\sqrt{2}}{4}$时取等号,
∴$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为-$\frac{1}{8}$.
故答案为:$-\frac{1}{8}$.
点评 本题考查了向量的三角形法则、向量数量积运算性质、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
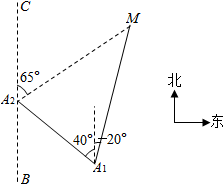 如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.
如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8\sqrt{3}}{3}$ | B. | $\frac{8\sqrt{3}}{4}$ | C. | $\frac{8}{3}$ | D. | $\frac{8\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinx)<f(1+sinx)<f(52+sinx) | B. | f(52+sinx)<f(sinx)<f(1+sinx) | ||
| C. | f(1+sinx)<f(sinx)≤f(52+sinx) | D. | f(1+sinx)<f(52+sinx)≤f(sinx) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com