
分析 (1)根据导数的几何意义求出函数在x=1处的导数,从而得到切线的斜率,建立等式关系,再根据切点在函数图象建立等式关系,解方程组即可求出a和b,从而得到函数f(x)的解析式;令f′(x)>0和令f′(x)<0,即可求出函数f(x)的单调区间
(2)先求出f′(x)=0的值,根据极值与最值的求解方法,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值.
解答 解:(1)f′(x)=12x2+2ax+b,f′(1)=12+2a+b=-12.①
又x=1,y=-12在f(x)的图象上,
∴4+a+b+5=-12.②
由①②得a=-3,b=-18,
∴f(x)=4x3-3x2-18x+5.
f′(x)=12x2-6x-18,
令f′(x)<0,得:12x2-6x-18<0,
可得-1<x<$\frac{3}{2}$,
∴函数f(x)的单调减区间为(-1,$\frac{3}{2}$),
令f′(x)>0,得:12x2-6x-18>0,
可得x<-1或x>$\frac{3}{2}$,
∴函数f(x)的单调增区间为(-∞,-1),($\frac{3}{2}$,+∞),
(2)f′(x)=12x2-6x-18=0,得x=-1,x=$\frac{3}{2}$,
f(-1)=16,f($\frac{3}{2}$)=-$\frac{61}{4}$,f(-3)=-76,f(1)=-13.
∴f(x)的最大值为16,最小值为-76.
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数求闭区间上函数的最值等基础题知识,考查运算求解能力,考查数形结合思想,属于基础题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
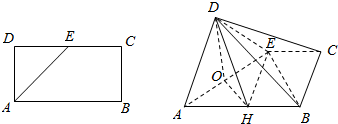 如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.
如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-2cos x | B. | f(x)=2cos x | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin 2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin 2x+cos 2x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{9}{4}$) | B. | (-∞,-$\frac{9}{4}$] | C. | [-$\frac{9}{4}$,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |x-a|≤3a | B. | |x-a|<3a | C. | |x-a|<0.03a | D. | |x-a|≤0.03a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
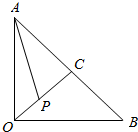 如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.
如图,△AOB为等腰直角三角形,OA=1,OC为斜边AB的高,点P在射线OC上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为$-\frac{1}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com