
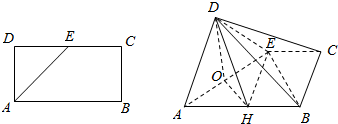
 如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.
如图所示,在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2$\sqrt{3}$,O,H分别为AE,AB的中点,平面BDE∩面DOH=l.分析 (1)要证:直线OH∥直线l,只需证明直线OH∥面BDE,只需证明OH∥EB即可;
(2)要证:面ADE⊥面ABCE,只需证明DO⊥AE,DO⊥OB 即 DO⊥面ABCE即可;
(3)VD-ABCE=$\frac{1}{3}$SABCE•DO,即可得出结论.
解答 (1)证明:∵O、H分别为AE、AB的中点
∴OH∥BE,又OH不在面BDE内
∴直线OH∥面BDE.
∵平面BDE∩面DOH=l,
∴直线OH∥直线l;
(2)证明:∵O为AE的中点,AD=DE,
∴DO⊥AE,
∵DO=$\sqrt{2}$,DB=2$\sqrt{3}$,BO2=10
∴DB2=DO2+BO2
∴DO⊥OB
∵AE和BO是相交直线
∴DO⊥面ABCE,
又OD在面ADE内
∴平面ADE⊥平面ABCE;
(3)解:VD-ABCE=$\frac{1}{3}$SABCE•DO=$\frac{1}{3}×(2+4)×2×\sqrt{2}$×$\frac{1}{2}$=2$\sqrt{2}$.
点评 本题考查了三棱锥的体积,线面平行的判定,线面垂直和面面垂直的性质、判定,熟练掌握空间直线与平面位置关系的定义、判定定理、性质定理是解答本题的关键,考查了空间想象能力、推理论证的能力.


科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 6 | C. | 4 | D. | 以上结论都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
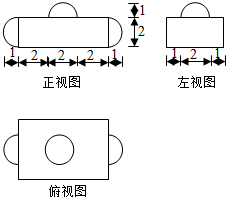
| A. | $48+\frac{4}{3}π$ | B. | 48+2π | C. | $48+\frac{8}{3}π$ | D. | 48+3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
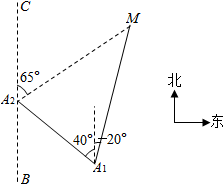 如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.
如图,一艘轮船按照北偏西40°的方向以30海里每小时的速度航行,一个灯塔原来在轮船的北偏东20°方向上,经过40分钟后,灯塔在轮船的北偏东65°方向上,则灯塔和轮船原来的距离为10($\sqrt{3}$+1)海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com