如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD是菱形，∠BAD=60°，AB=2，PD=
，O为AC与BD的交点，E为棱PB上一点．
（Ⅰ）证明：平面EAC⊥平面PBD；
（Ⅱ）若PD∥平面EAC，求三棱锥P﹣EAD的体积．
阅读快车系列答案科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（新课标1卷精编版） 题型：解答题
某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：
记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），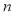
表示购机的同时购买的易损零件数.
（Ⅰ）若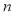=19，求y与x的函数解析式；
（Ⅱ）若要求“需更换的易损零件数不大于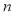”的频率不小于0.5，求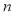的最小值；
（Ⅲ）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？
查看答案和解析>>
科目：高中数学 来源：2016届山东省莱芜市高三上期末文科数学试卷（解析版） 题型：选择题
已知函数f（x）是定义在R上的偶函数，且当x≥0时，f（x）=ln（1﹣x），则函数f（x）的大致图象为（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2016届湖南省邵阳市高三上期末文科数学试卷（解析版） 题型：解答题
已知曲线C的参数方程为
，直线l的极坐标方程为ρsin（θ+
）=﹣2
．
（1）写出曲线C的普通方程和直线l的直角坐标方程；
（2）设点P为曲线C上的动点，求点P到直线l距离的最大值．
查看答案和解析>>
科目：高中数学 来源：2016届湖南省邵阳市高三上期末文科数学试卷（解析版） 题型：选择题
将直径为2的半圆绕直径所在的直线旋转半周而形成的曲面所围成的几何体的表面积为（ ）
A．2π B．3π C．4π D．6π
查看答案和解析>>
科目：高中数学 来源：2016年全国普通高等学校招生统一考试文科数学（新课标3卷精编版） 题型：选择题
已知O为坐标原点，F是椭圆C：
的左焦点，A，B分别为C的左，右顶点.P为C上一点，且
轴.过点A的直线l与线段
交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为
（A）
（B）
（C）
（D）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，其中x，y是实数，则
（C）
（D）2
，则a与b夹角的大小为_________.