练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图a是某市参加2012年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为、、…、[如表示身高（单位：cm）在内的学生人数]．图b是统计图a中身高在一定范围内学生人数的一个算法流程图．现要统计身高在（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是（ ）

    A.B.C.D.

    【答案】B

    【解析】

    由题目要求可知：该程序的作用是统计身高在（含160cm，不含180cm）的学生人数，由图1可知应该从第四组数据累加到第七组数据，故i值应小于8．

    现要统计的是身高在之间的学生的人数，即是要计算、、、的和，

    当时就会返回进行叠加运算，

    当将数据直接输出，

    不再进行任何的返回叠加运算，故．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】同程旅游随机调查了年龄在（单位：岁）内的1250人的购票情况，其中50岁以下（不包含50岁）的有900人，50岁以上（包含50岁）的有350人，由调查数据的统计结果显示，有的人参与网上购票，网上购票人数的频率分布直方图如下图所示.

    （1）已知年龄在，，的网上购票人数成等差数列，求的值；

    （2）根据题目数据填写列联表，并根据填写数据判断能否在犯错误的概率不超过0.001的前提下，认为网上购票与年龄有关系？

    50岁以下

    50岁以上

    总计

    参与网上购票

    不参与网上购票

    总计

    附：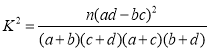

    0.010

    0.005

    0.001

    6.635

    7.879

    10.828

    （3）为鼓励大家网上购票，该平台常采用购票就发放酒店入住代金券的方法进行促销，具体做法如下：年龄在岁的每人发放20元，其余年龄段的每人发放50元，先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取10人，并在这10人中随机抽取3人进行回访调查，求此3人获得代金券的金额总和的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，.

    （1）若曲线在处的切线与曲线相切，求的值；

    （2）当时，函数的图象恒在函数的图象的下方，求的取值范围；

    （3）若函数恰有2个不相等的零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （1）为曲线上的动点，点在线段上，且满足，求点的轨迹的直角坐标方程；

    （2）设点的极坐标为，点在曲线上，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知椭圆E：（）过点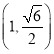，其心率等于.

    （1）求椭圆E的标准方程；

    （2）若A，B分别是椭圆E的左，右顶点，动点M满足，且椭圆E于点P.

    ①求证：为定值：

    ②设与以为直径的圆的另一交点为Q，求证：直线经过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲居住在城镇的处,准备开车到单位处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如：算作两个路段：路段发生堵车事件的概率为,路段发生堵车事件的概率为).

    (1)请你为甲选择一条由到的最短路线

    (即此人只选择从西向东和从南向北的路线),

    使得途中发生堵车事件的概率最小；

    (2)设甲在路线中遇到的堵车次数为随机变量,求的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知是直角梯形，且，平面平面，， ， ，是的中点.

    （1）求证：平面；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国在欧洲的某孔子学院为了让更多的人了解中国传统文化，在当地举办了一场由当地人参加的中国传统文化知识大赛，为了了解参加本次大赛参赛人员的成绩情况，从参赛的人员中随机抽取名人员的成绩（满分100分）作为样本，将所得数据进行分析整理后画出频率分布直方图如下图所示，已知抽取的人员中成绩在[50,60)内的频数为3.

    （1）求的值和估计参赛人员的平均成绩（保留小数点后两位有效数字）；

    （2）已知抽取的名参赛人员中，成绩在[80,90)和[90,100]女士人数都为2人，现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取1人，求这两人恰好都为女士的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在坐标原点O，焦点在x轴上，离心率为的椭圆过点.

    （1）求椭圆的方程；

    （2）设不过原点O的直线l与该椭圆交于P，Q两点，满足直线OP，PQ，OQ的斜率依次成等比数列，若的面积为，求直线l与y轴交点的坐标.

    查看答案和解析>>

    同步练习册答案