
分析 分别化简解出命题p,q的取值范围组成的集合A,B,由¬p是¬q的充分不必要条件,可得:p是q的必要不充分条件,因此B?A.即可得出.
解答 解:对于命题p:由$\frac{1}{x-2}$<1,可得:x-2<0,或$\left\{\begin{array}{l}{x-2>0}\\{1<x-2}\end{array}\right.$,
解得:x<2,或x>3.
∴A={x|x<2,或x>3}.
对于命题q:|x-a|<1,解得-1+a<x<a+1.
∴B=(a-1,a+1).
由¬p是¬q的充分不必要条件,可得:p是q的必要不充分条件.
∴B?A,
即a+1≤2或a-1≥3.
解得a≤1或a≥4.
∴实数a的取值范围是(-∞,1]∪[4,+∞).
点评 本题考查了简易逻辑的判断方法、不等式的解法、集合之间的关系,考查了推理能力与计算能力,属于中档题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
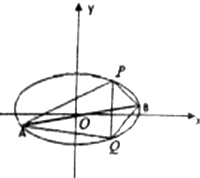 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com