
已知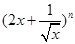 的展开式前两项的二项式系数的和为10.
的展开式前两项的二项式系数的和为10.
(1) 求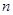 的值.
的值.
(2) 这个展开式中是否有常数项?若有,将它求出,若没有,请说明理由.
科目:高中数学 来源: 题型:解答题
现有5名男生和3名女生.
(1)若3名女生必须相邻排在一起,则这8人站成一排,共有多少种不同的排法?
(2)若从中选5人,且要求女生只有2名, 站成一排,共有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用1、2、3、4四个数字可重复地任意排成三位数,并把这些三位数由小到大排成一个数列{an}.
(1)写出这个数列的第8项;
(2)这个数列共有多少项?
(3)若an=341,求n.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
规定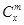 =
=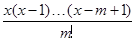 ,其中
,其中 是正整数,且
是正整数,且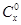 =1,这是组合数
=1,这是组合数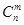 (
(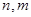 是正整数,且
是正整数,且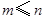 )的一种推广.
)的一种推广.
(1)求 的值;
的值;
(2)设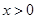 ,当
,当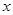 为何值时,
为何值时,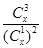 取得最小值?
取得最小值?
(3)组合数的两个性质:①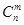 =
=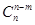 ; ②
; ②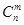 +
+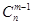 =
=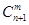
是否都能推广到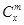 (
( 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com