
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据方程特点得:以-x代替 x,以-y代替y,方程也不变,说明曲线关于x轴、y轴、原点对称;又x2=(1-y2)•(1+y2)≥(1-y2),即:x2≥(1-y2)即x2+y2≥1,说明曲线上任意一点到原点的距离都大于或等于1,故封闭曲线面积大于π,结合正方形的面积;以及两点之间线段最短,综合可得答案.
解答 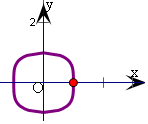 解:以-x代替 x,方程不变,以-y代替y,方程也不变,
解:以-x代替 x,方程不变,以-y代替y,方程也不变,
同时以x代替 x、-y代替y,方程也不变,
说明曲线关于x轴、y轴、原点对称,故①正确;
又∵x2=(1-y2)•(1+y2)≥(1-y2)∴x2+y2≥1,
∴曲线上任意一点到原点的距离都大于或等于1,(当且仅当y=0时,等于1)
故②正确;
由②可得,曲线C所围成图形的面积S满足大于单位圆的面积,小于边长为2的正方形的面积,
即π<S<4,故④正确;
曲线C在每一段的长都大于$\sqrt{2}$,故由对称性满足l>4$\sqrt{2}$,故③正确.
故选:A.
点评 本题考查曲线的性质,命题的真假判断,注意运用不等式的性质和数形结合的思想方法,考查推理能力和判断能力,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )| A. | 6 | B. | 25 | C. | 100 | D. | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
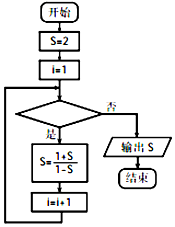 某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )
某程序框图如图所示,该程序运行后若输出S的值是2,则判断框内可填写( )| A. | i≤2015? | B. | i≤2016? | C. | i≤2017? | D. | i≤2018? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知等差数列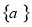 ,
, 为数列
为数列 的前
的前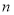 项和,若
项和,若 (
( ),记数列
),记数列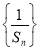 的前
的前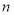 项和为
项和为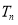 ,则
,则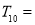 ( )
( )
A.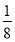 B.
B.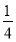
C. D.
D.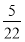
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:解答题
在直角坐标系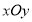 中,以原点
中,以原点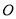 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线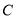 的极坐标方程为
的极坐标方程为 .
.
(1)求曲线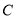 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设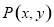 是曲线
是曲线 上的动点,求
上的动点,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
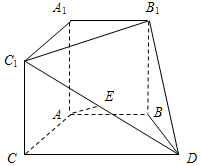 在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.
在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com