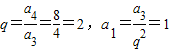已知等比数列{an}的各项都是正数,前n项和为Sn,
且a3=4,S4=S3+8,求:(1)等比数列{an}的通项公式;(2)若bn=nan,求数列{bn}的前n项和 Tn.
【答案】
分析:(1)因为已知数列{a
n}为等比数列,所以只要找到首项和公比即可,利用S
4=S
3+8,S
4-S
2=a
4,得a
4=8,再根据
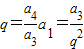
求a
1和q,代入等比数列通项公式,即可得等比数列{a
n}的通项公式.
(2)把(1)中所求a
n=2
n-1代入b
n=na
n,,可得数列{b
n}的通项公式为b
n=n•2
n-1,然后利用错位相减,可以求出数列{b
n}的前n项和 T
n.
解答:解:(1)∵S
4=S
3+8,∴a
4=S
4-S
3=8,又∵a
3=4,
∴
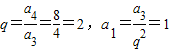
∴等比数列{a
n}的通项公式a
n=2
n-1.
(2)由(1)知:数列{a
n}的首项为1,公比为2,a
n=2
n-1,b
n=n•2
n-1,
∴b
n=n•2
n-1,
∴T
n=b
1+b
2+b
3…+b
n=1+2•2+3•2
2+…+n•2
n-12T
n=2+2•2
2+3•2
3+…+(n-1)•2
n-1+n•2
n∴T
n=(n-1)2
n+1
点评:本题考查了等比数列的通项公式,以及错位相减求和,做题时要细心.

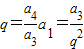 求a1和q,代入等比数列通项公式,即可得等比数列{an}的通项公式.
求a1和q,代入等比数列通项公式,即可得等比数列{an}的通项公式.