
分析 根据题意,将原问题转化为函数f(x)=kx2+kx+1>0恒成立;分两种情况讨论:①、k=0时,易得f(x)=1>0,符合题意;②、k≠0时,若f(x)=kx2+kx+1>0恒成立,必有k>0且k2-4k<0,解可得k的范围;综合2种情况即可得答案.
解答 解:根据题意,不等式kx2+kx+1>0可以转化为函数f(x)=kx2+kx+1>0恒成立;
①、k=0时,f(x)=1>0,符合题意;
②、k≠0时,若f(x)=kx2+kx+1>0恒成立,
必有k>0且k2-4k<0,
解可得0<k<4;
综合可得k的取值范围是0≤k<4;
故答案为:0≤k<4.
点评 本题考查不等式的恒成立问题,注意分析k=0时的情况.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
| 广告费用x(万元) | 3 | 4 | 5 | 6 |
| 年销售量t(件) | 25 | 30 | 40 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
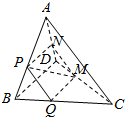 如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )| A. | AC⊥BD | B. | AC∥截面PQMN | ||
| C. | AC=BD | D. | 异面直线PM与BD所成的角为45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com