
已知椭圆 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于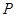 ,
,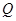 两点,问:△
两点,问:△ 的周长是否为定值?如果是,求出定值;如果不是,说明理由.
的周长是否为定值?如果是,求出定值;如果不是,说明理由.
(1)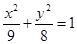 ;(2)详见解析
;(2)详见解析
解析试题分析:(1)根据点在曲线上可代入方程,再根据椭圆中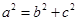 ,解方程组可得
,解方程组可得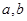 的值。从而可得椭圆方程。法二,还可根据椭圆的定义椭圆上点到两焦点的距离为
的值。从而可得椭圆方程。法二,还可根据椭圆的定义椭圆上点到两焦点的距离为 直接求得
直接求得 ,再根据
,再根据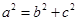 求
求 。(2)设
。(2)设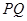 的方程为
的方程为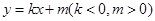 ,根据与圆相切可得
,根据与圆相切可得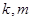 间的关系。再将直线与椭圆方程联立消掉
间的关系。再将直线与椭圆方程联立消掉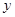 整理为关于
整理为关于 的一元二次方程,可得根与系数的关系。由直线与圆锥曲线的相交弦公式可得
的一元二次方程,可得根与系数的关系。由直线与圆锥曲线的相交弦公式可得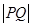 ,再根据两点间距离可求
,再根据两点间距离可求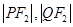 ,将三边长相加,根据前边得到的
,将三边长相加,根据前边得到的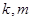 间的关系问题即可得证。
间的关系问题即可得证。
试题解析:(1)『解法1』:
(1)由题意,得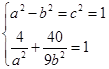 ,2分
,2分
解得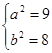 4分
4分
∴椭圆方程为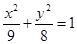 .5分
.5分
『解法2』: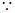 右焦点为
右焦点为 ,
,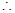
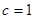
左焦点为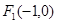 ,点
,点 在椭圆上
在椭圆上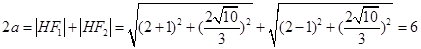
所以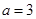 ,
,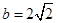
所以椭圆方程为 5分
5分
(2)『解法1』:
由题意,设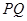 的方程为
的方程为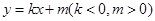
∵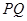 与圆
与圆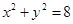 相切
相切
∴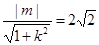 ,即
,即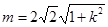 6分
6分
由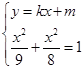 ,得
,得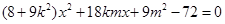 7分
7分
设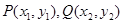 ,则
,则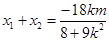 ,
,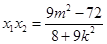 8分
8分
∴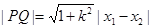
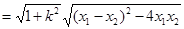
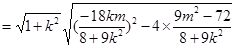
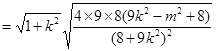
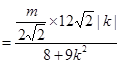
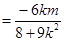 10分
10分
又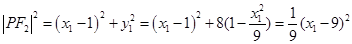
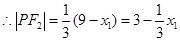
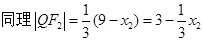
∴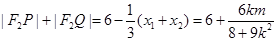 11分
11分
∴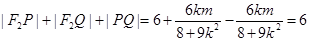 (定值)12分
(定值)12分
『解法2』:
设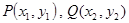 ,
,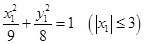
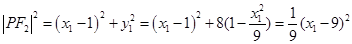
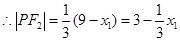 8分
8分
连接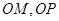 ,由相切条件知:
,由相切条件知: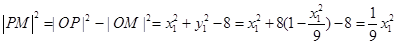
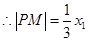
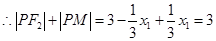 10分
10分
同理可求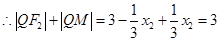
所以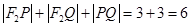 为定值.12分
为定值.12分
考点:1椭圆的标准方程;2直线和圆锥曲线的相交弦问题;3直线和圆的位置关系。


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
已知中心在坐标原点,焦点在 轴上的椭圆过点
轴上的椭圆过点 ,且它的离心率
,且它的离心率 .
.
(1)求椭圆的标准方程;
(2)与圆 相切的直线
相切的直线 交椭圆于
交椭圆于 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 的短半轴长为
的短半轴长为 ,动点
,动点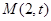
 在直线
在直线 (
( 为半焦距)上.
为半焦距)上.
(1)求椭圆的标准方程;
(2)求以 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;
(3)设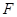 是椭圆的右焦点,过点
是椭圆的右焦点,过点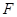 作
作 的垂线与以
的垂线与以 为直径的圆交于点
为直径的圆交于点 ,
,
求证:线段 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线 与x轴交于点B且与直线
与x轴交于点B且与直线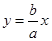 交于点C,点O为坐标原点,
交于点C,点O为坐标原点, ,过点F的直线
,过点F的直线 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.
(1)求椭圆的方程;
(2)求 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知抛物线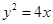 .
.
(1)若圆心在抛物线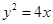 上的动圆,大小随位置而变化,但总是与直线
上的动圆,大小随位置而变化,但总是与直线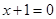 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;
(2)抛物线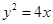 的焦点为
的焦点为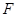 ,若过
,若过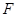 点的直线与抛物线相交于
点的直线与抛物线相交于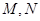 两点,若
两点,若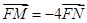 ,求直线
,求直线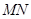 的斜率;
的斜率;
(3)若过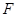 点且相互垂直的两条直线
点且相互垂直的两条直线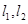 ,抛物线与
,抛物线与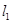 交于点
交于点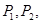 与
与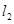 交于点
交于点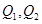 .
.
证明:无论如何取直线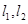 ,都有
,都有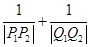 为一常数.
为一常数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,一条准线方程为x=
,一条准线方程为x=
(1)求椭圆C的方程;
(2)设G、H为椭圆C上的两个动点,O为坐标原点,且OG⊥OH.
①当直线OG的倾斜角为60°时,求△GOH的面积;
②是否存在以原点O为圆心的定圆,使得该定圆始终与直线GH相切?若存在,请求出该定圆方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图;.已知椭圆C: 的离心率为
的离心率为 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.
(1)求椭圆C的方程;
(2)求 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与 轴交于点R,S,O为坐标原点. 试问;是否存在使
轴交于点R,S,O为坐标原点. 试问;是否存在使 最大的点P,若存在求出P点的坐标,若不存在说明理由.
最大的点P,若存在求出P点的坐标,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知双曲线的焦点在x轴上,两个顶点间的距离为2,焦点到渐近线的距离为 .
.
(1)求双曲线的标准方程;
(2)写出双曲线的实轴长、虚轴长、焦点坐标、离心率、渐近线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com