
| A. | {0,-1} | B. | {0,$\frac{1}{2}}\right\$} | C. | {-1,$\frac{1}{2}}\right\$} | D. | {-1,0,$\frac{1}{2}}\right\$} |
分析 设直线方程为:y=k(x+2)+1,代入抛物线方程得k2x2+(4k2+2k-4)x+4k2+4k+1=0(*),直线与抛物线只有一个公共点等价于(*)只有一个根,由此能求出结果.
解答 解:经过点P(-2,1)且斜率为k的直线l为:y=k(x+2)+1,
代入抛物线方程y2=4x整理可得k2x2+(4k2+2k-4)x+4k2+4k+1=0(*),
直线与抛物线只有一个公共点等价于(*)只有一个根,
①k=0时,y=1符合题意;
②k≠0时,△=(4k2+2k-4)2-4k2(4k2+4k+1)=0,整理,得2k2+k-1=0,
解得k=$\frac{1}{2}$或k=-1.
综上可得,k=$\frac{1}{2}$或k=-1或k=0时,直线l与抛物线只有一个公共点,
故k∈{-1,0,$\frac{1}{2}}\right\$},
故选:D.
点评 本题主要考查直线和抛物线位置关系的应用,要对k进行分类讨论,注意直线与抛物线的位置关系的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{e}$-1 | D. | 1-$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢数学课程 | 不喜欢数学课程 | 合计 | |
| 男 | 45 | 75 | 120 |
| 女 | 45 | a | 180 |
| 合计 | 90 | b | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
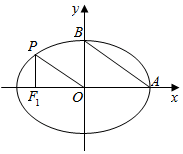 如图,椭圆$\frac{x^2}{a^2$+$\frac{y^2}{b^2}$=1(a>b>0)与x轴、y轴的正半轴相交于A、B,过椭圆上一点P作x轴的垂线,垂足恰为左焦点F1,OP∥AB.
如图,椭圆$\frac{x^2}{a^2$+$\frac{y^2}{b^2}$=1(a>b>0)与x轴、y轴的正半轴相交于A、B,过椭圆上一点P作x轴的垂线,垂足恰为左焦点F1,OP∥AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 身高一定是146cm | B. | 身高在146cm以上 | C. | 身高在146cm以下 | D. | 身高在146cm左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com