练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．若正数a、b满足a+2b=1，则$\frac{2}{a}$+$\frac{1}{b}$的最小值是8．

    分析 利用“乘1法”与基本不等式的性质即可得出．

    解答 解：∵正数a、b满足a+2b=1，
    则$\frac{2}{a}$+$\frac{1}{b}$=（a+2b）$（\frac{2}{a}+\frac{1}{b}）$=4+$\frac{4b}{a}+\frac{a}{b}$≥4+2$\sqrt{\frac{4b}{a}×\frac{a}{b}}$=8，当且仅当a=2b=$\frac{1}{2}$时取等号．
    ∴$\frac{2}{a}$+$\frac{1}{b}$的最小值是8．
    故答案为：8．

    点评 本题考查了“乘1法”与基本不等式的性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．已知数列{an}中，a1=1，且an+1=2an+1，则a4=（　　）
    A．7B．9C．15D．17

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．在复平面内，表示复数2-3i（i是虚数单位）的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．经过点P（-2，1）且斜率为k的直线l与抛物线y2=4x只有一个公共点，则k的取值范围为（　　）
    A．{0，-1}B．{0，$\frac{1}{2}}\right\$}C．{-1，$\frac{1}{2}}\right\$}D．{-1，0，$\frac{1}{2}}\right\$}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列四个命题一定正确的是（　　）
    A．算法的三种基本结构是顺序结构、条件结构，循环结构
    B．用样本频率分布估计总体频率分布的过程中，总体容量越大，估计越精确
    C．一组数据的方差为3，将这组数据中的每一个数据都扩大到原来的3倍，所得的新数据组的方差还是3
    D．有50件产品编号从1到50，现在从中抽取5件检验，用系统抽样确定所抽取的编号为5，15，20，35，40

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

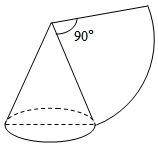
    3．如图，一个圆锥的侧面展开图是圆心角为90°面积为S1的扇形，若圆锥的全面积为S2，则$\frac{S_2}{S_1}$等于$\frac{5}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题中错误的是（　　）
    A．若m∥n，m⊥α，则n⊥αB．若m⊥α，m∥n，n∥β，则α⊥β
    C．若m⊥α，m⊥β，则α∥βD．若m∥α，n∥β，α∥β，则m∥n

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知数列{an}的各项均是正数，其前n项和为Sn，满足Sn=4-an．
    （1）求数列{an}的通项公式；
    （2）设bn=$\left\{\begin{array}{l}{{log}_{{\frac{1}{2}}^{{a}_{n}}}}（n为奇数）\\{{a}_{n}（n为偶数）}\end{array}\right.$（n∈N*），求数列{bn}的前2n项和T2n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．二项式（x+$\frac{1}{\root{3}{x}}$-4y）7展开式中不含x的项的系数之和为-47-44${∁}_{7}^{4}$．

    查看答案和解析>>

    同步练习册答案