
����Ŀ�����г����飬ij��Ʒÿ�ֵļ۸�Ϊx��1��x��14����Ԫʱ������Ʒ���¹�����Ϊy1�֣�y1=ax+ ![]() a2��a��a��0������������Ϊy2�֣�y2=��
a2��a��a��0������������Ϊy2�֣�y2=�� ![]() x2��
x2�� ![]() x+1��������Ʒ�����������ڹ�����ʱ�����������ڹ�������������Ʒ�������������ڹ�����ʱ������������������������Ʒ�������۶��������������۸�ij˻���
x+1��������Ʒ�����������ڹ�����ʱ�����������ڹ�������������Ʒ�������������ڹ�����ʱ������������������������Ʒ�������۶��������������۸�ij˻���
��1����֪a= ![]() ����ij�¸���Ʒ�ļ۸�Ϊx=7������Ʒ�ڸ��µ����۶��ȷ��1Ԫ����
����ij�¸���Ʒ�ļ۸�Ϊx=7������Ʒ�ڸ��µ����۶��ȷ��1Ԫ����
��2�����������빩�������ʱ�ļ۸�Ϊ����۸�������Ʒ�ľ���۸���ÿ��6��Ԫ����ʵ��a��ȡֵ��Χ��
���𰸡�
��1���⣺��a= ![]() ��x=7ʱ��y1=
��x=7ʱ��y1= ![]() ��7+
��7+ ![]() ����
���� ![]() ��2��
��2�� ![]() =1+
=1+ ![]() ��
�� ![]() =
= ![]() ��
��
y2=�� ![]() ����
���� ![]() ��2��
��2�� ![]() ��
�� ![]() +1=
+1= ![]() ��
��
��y1��y2��
��������۶�Ϊ7�� ![]() ��104��50313��Ԫ��
��104��50313��Ԫ��
��2���⣺��f��x��=y1��y2= ![]() x2+��
x2+�� ![]() +a��x��a��1��
+a��x��a��1��
��f��x����[6��14��������㣬
��a��0����f��0��=��a��1��0����f��x����ͼ�����ϣ�
��f��x����[6��14����ֻ��1����㣬
�� ![]() ����
���� 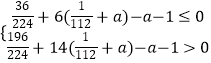 ��
��
��ã�0��a�� ![]()
����������1������y1 �� y2 �� �Ƚϴ�Сȷ�����������ټ������۶��2����f��x��=y1��y2 �� ��f��x����[6��14��������㣬�������Ĵ����Զ����в���ʽ����a�ķ�Χ��


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=ln��ax+b��+x2��a��0����
��1��������y=f��x���ڵ㣨1��f��1�����������߷���Ϊy=x����a��b��ֵ��
��2����f��x����x2+x���������ab�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���趨����R�ϵ�ż����y=f��x�������������t��R����f��t��=f��2��t������x�ʣ�0��1]ʱ��f��x��= ![]() ��a=f��
��a=f�� ![]() ����b=f��
����b=f�� ![]() ����c=f��
����c=f�� ![]() ������ ��
������ ��
A.b��c��a
B.a��b��c
C.c��a��b
D.b��a��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=x3��ax2+1�ڣ�1��3���ڵ����ݼ�����ʵ��a�ķ�Χ�ǣ� ��
A.[ ![]() ��+�ޣ�
��+�ޣ�
B.�����ޣ�3]
C.��3�� ![]() ��
��
D.��0��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=mln��x+1����nx�ڵ㣨1��f��1��������������y�ᴹֱ���� ![]() ������ m��n��R��
������ m��n��R��
������m��n��ֵ�������f��x���ĵ������䣻
������g��x��=��x2+2x��ȷ���Ǹ�ʵ��a��ȡֵ��Χ��ʹ����ʽf��x��+x��ag��x����[0��+�ޣ��Ϻ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ����ĸ����ǣ� �� �ٶ�������p��x��R��ʹ��x2+x+1��0����Vp��x��R������x2+x+1��0��
�����⡰��֪x��y��R����x+y��3����x��2��y��1���������⣻
�ۻع�ֱ�ߵ�б�ʵĹ���ֵΪ1.23�������������Ϊ��4��5������ع�ֱ�߷���Ϊ ![]() =1.23x+0.08��
=1.23x+0.08��
��m=3��ֱ�ߣ�m+3��x+my��2=0��ֱ��mx��6y+5=0���ഹֱ�ij�Ҫ������
A.1
B.3
C.2
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪m��0��n��0�� ![]() +mn����СֵΪt��
+mn����СֵΪt��
��1����tֵ
��2�������x�IJ���ʽ|x��1|��t+2x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ִ����ͼ��ʾ�ij����ͼ���������a=16��b=4���������n=�� �� 
A.4
B.5
C.6
D.7
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com