
已知数列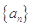 的首项
的首项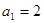 ,且对任意
,且对任意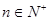 都有
都有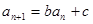 (其中
(其中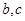 为常数).
为常数).
(1)若数列 为等差数列,且
为等差数列,且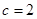 ,求
,求 的通项公式.
的通项公式.
(2)若数列 是等比数列,且
是等比数列,且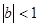 ,从数列
,从数列 中任意取出相邻的三项,均能按某种顺序排成等差数列,求
中任意取出相邻的三项,均能按某种顺序排成等差数列,求 的前
的前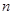 项和
项和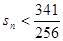 成立的
成立的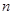 的取值的集合.
的取值的集合.
(1)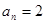 或
或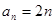 ;(2){2,4,6,8} .
;(2){2,4,6,8} .
解析试题分析:(1)对实数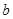 分类讨论,①
分类讨论,①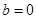 ,
,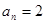 ;②
;②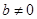 时,根据等差数列的定义,可知
时,根据等差数列的定义,可知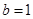 ,公差
,公差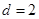 ,则
,则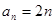 ;(2)若数列
;(2)若数列 为等比数列,则
为等比数列,则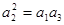 ,即
,即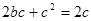 ,因此
,因此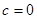 (注意
(注意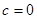 是容易漏掉的)或
是容易漏掉的)或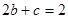 , 在这
, 在这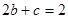 情况下,可得
情况下,可得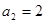 ,故
,故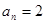 不满足
不满足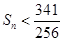 ,因此只有
,因此只有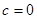 满足条件,由任相邻的三项均能按某种顺序排成等差数列,可分为以下三种情况:①
满足条件,由任相邻的三项均能按某种顺序排成等差数列,可分为以下三种情况:①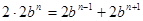 ;②
;②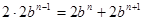 ;③
;③ ,分别求出
,分别求出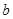 看是否满足条件,由满足条件的
看是否满足条件,由满足条件的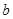 结合
结合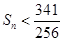 确定
确定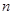 的取值的个数.
的取值的个数.
(1)当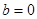 时,
时,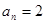 符合题意,
符合题意,
当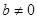 时,由于数列
时,由于数列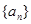 是等差数列且
是等差数列且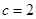 ,所以
,所以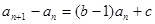 为常数,故
为常数,故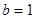 ,得
,得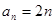 ,
,
所以,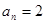 或
或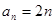 .(6分)(只求得一个得3分)
.(6分)(只求得一个得3分)
(2)由数列 为等比数列,所以
为等比数列,所以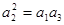 得
得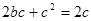
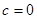 或
或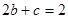 , (8分)
, (8分)
若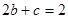 得
得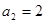 ,故
,故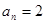 不满足
不满足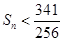
所以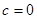 ,得
,得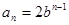 .
.
由任相邻的三项均能按某种顺序排成等差数列,即
若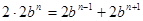 得
得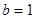 (舍).
(舍).
若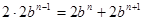 得
得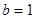 (舍)或
(舍)或 (舍),
(舍),
若 得
得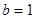 舍或
舍或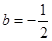 ,
,
故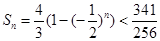 得
得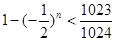
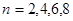 即所求值的集合为{2,4,6,8} (13分)
即所求值的集合为{2,4,6,8} (13分)
考点:等差数列、等比数列的性质.


科目:高中数学 来源: 题型:解答题
设等比数列{an}的前n项和为Sn,已知an + 1 = 2Sn + 2 (n∈N*).
(1)求数列{an}的通项公式;
(2)在an与an + 1之间插入n个数,使这n + 2个数组成一个公差为dn的等差数列.
①在数列{dn}中是否存在三项dm,dk,dp (其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②求证: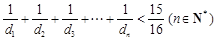 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等差数列{an}前三项的和为-3,前三项的积为8.
(1) 求等差数列{an}的通项公式;
(2) 若数列{an}单调递增,求数列{an}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an}是公差不为0的等差数列,a1=2,且a2,a3,a4+1成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=an+2an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果数列 满足:
满足: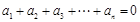 且
且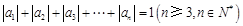 ,则称数列
,则称数列 为
为 阶“归化数列”.
阶“归化数列”.
(1)若某4阶“归化数列” 是等比数列,写出该数列的各项;
是等比数列,写出该数列的各项;
(2)若某11阶“归化数列” 是等差数列,求该数列的通项公式;
是等差数列,求该数列的通项公式;
(3)若 为n阶“归化数列”,求证:
为n阶“归化数列”,求证: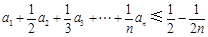 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列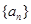 的各项均为正数,记
的各项均为正数,记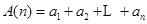 ,
,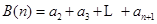 ,
,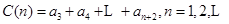 .
.
(1)若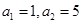 ,且对任意
,且对任意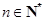 ,三个数
,三个数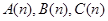 组成等差数列,求数列
组成等差数列,求数列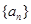 的通项公式.
的通项公式.
(2)证明:数列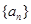 是公比为
是公比为 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意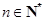 ,三个数
,三个数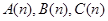 组成公比为
组成公比为 的等比数列.
的等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com