练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．函数y=-2ax+b与函数y=ax2-2bx+c在同一坐标系内的图象只可能是（　　）
    A．B．C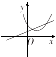．D．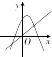

    分析 根据a与b的正负来讨论二次函数的开口方向向上或向下、对称轴在y轴的左侧或右侧，利用排除法得到正确答案即可．

    解答 解：当a＞0时，y=ax2-2bx+c开口向上，y=-2ax+b为减函数，故排除B，C
    当a＜0，b＞0时，y=ax2-2bx+c开口向下，对称轴x=$\frac{b}{a}$＜0，y=-2ax+b为增函数，与y轴交于负半轴，故排除D
    当a＞0，b＞0时，y=ax2-2bx+c开口向下，对称轴x=$\frac{b}{a}$＞0，y=-2ax+b为增函数，与y轴交于负半轴，A符合，
    故选：A

    点评 此题的解题思路是假设一次函数的图象正确来判断二次函数的正确与否，做题的方法是排除法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．若随机变量ξ～B（n，P），Eξ=15，Dξ=11.25，则n=（　　）
    A．45B．50C．55D．60

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．在2016年高考志愿填报中，三（1）班有60人，其中填报北京航空航天大学的有15人，填报南京航空航天大学的有20人，填报以上两所大学的人数为30（每人可填报多个平行志愿），则下列说法中错误的是（　　）
    A．本班没有填报北航与南航的有30人B．填报北航但没有填报南航的有10人
    C．填报南航但没有填报北航的有15人D．同时填报北航与南航的学生有10人

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，$|{\vec a}|=1$且$|{2\vec a-\vec b}|=2$，求$|{\vec b}|$0或2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．如图，在△ABC中，AB=BC=2，∠ABC=30°，AD是边BC上的高，则$\overrightarrow{AD}$•$\overrightarrow{AC}$的值等于1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若定义在R上的函数f（x），满足f（x+2）=f（x），且当x∈[-1，1]时，f（x）=x2，函数g（x）=$\left\{\begin{array}{l}{lo{g}_{3}（x-1），x＞1}\\{{2}^{x}，x≤1}\end{array}\right.$，则函数h（x）=f（x）-g（x）在区间[-4，5]内的零点的个数为（　　）
    A．7B．8C．9D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设函数f（x）=$\frac{x}{x+3}$（x＞0），观察：f1（x）=f（x）=$\frac{x}{x+3}$，f2（x）=f（f1（x））=$\frac{x}{4x+9}$，
    f3（x）=f（f2（x））=$\frac{x}{13x+27}$，f4（x）=f（f3（x））=$\frac{x}{40x+81}$…，根据以上事实，由归纳推理可得：当n∈N*，n≥2时，fn（x）=f （fn-1（x））=$\frac{x}{{\frac{{{3^n}-1}}{2}x+{3^n}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=$\sqrt{3}$sin（x+$\frac{π}{4}$），x∈R，若f（θ）+f（-θ）=$\frac{3}{2}$，θ∈（0，$\frac{π}{2}$），求tanθ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．函数y=loga（x-1）+2（a＞0且a≠1）恒过定点（2，2）．

    查看答案和解析>>

    同步练习册答案