练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．若向量$\overrightarrow a$=（2，m），$\overrightarrow b$=（1，$\sqrt{3}}$），且$\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$垂直，则实数m的值为0．

    分析 根据平面向量的坐标表示与运算，列出方程，求解即可．

    解答 解：向量$\overrightarrow a$=（2，m），$\overrightarrow b$=（1，$\sqrt{3}}$），
    ∴$\overrightarrow a+\overrightarrow b$=（3，m+$\sqrt{3}$），
    $\overrightarrow a-\overrightarrow b$=（1，m-$\sqrt{3}$）；
    又（$\overrightarrow a+\overrightarrow b$）⊥（$\overrightarrow a-\overrightarrow b$），
    ∴（$\overrightarrow{a}$+$\overrightarrow{b}$）•（$\overrightarrow{a}$-$\overrightarrow{b}$）=3×1+（m+$\sqrt{3}$）（m-$\sqrt{3}$）=0，
    解得m=0．
    故答案为：0．

    点评 本题考查了平面向量的坐标表示与运算问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．一个几何体的三视图如图，则该几何体的体积为（　　）
    A．32+$\frac{16π}{3}$B．32+$\frac{64π}{3}$C．64+$\frac{16π}{3}$D．64+$\frac{64π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

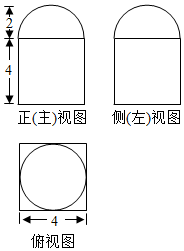
    1．某几何体的三视图如图所示，其中俯视图中的弧线是半径为1的四分之一个圆弧，则该几何体的体积为（　　）
    A．1B．2πC．1-$\frac{π}{4}$D．1-$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

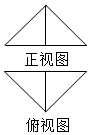    18．把边长为2的正方形ABCD沿对角线BD折起并连接AC形成三棱锥C-ABD，其正视图、俯视图均为等腰直角三角形（如图所示），则三棱锥C-ABD的表面积为4+2$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的一个焦点与抛物线y2=16x的焦点重合，且双曲线的离心率等于2，则该双曲线的渐近线方程为（　　）
    A．$y=±\sqrt{3}x$B．$y=±\frac{{\sqrt{3}}}{3}x$C．$y=±\sqrt{2}x$D．y=±2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设a=n（n-1）（n-2）…（n-50），则a可表示为（　　）
    A．${A}_{n}^{51}$B．${C}_{n}^{51}$C．${A}_{n}^{50}$D．${C}_{n}^{50}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知等比数列{an}满足a1=3，a1+a3+a5=21，则a3+a5+a7=42．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

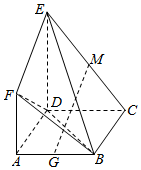    18．如图，ABCD为边长为2的正方形，DE⊥平面ABCD，AF∥DE，DE=2AF，BE与平面ABCD所成角为45°，G，H分别为AB，EC的中点．（1）求证：GH∥平面ADEF；
    （2）求二面角F-BD-E的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知球的直径SC=4，A，B是该球面上的两点，∠AOB=90°，O为球心，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为$\frac{8}{3}$．

    查看答案和解析>>

    同步练习册答案