
(本小题满分12分)如图, 四棱柱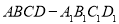 的底面ABCD是正方形,
的底面ABCD是正方形,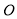 为底面中心,
为底面中心,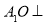 平面
平面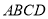 ,
,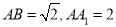 .
.

(1)证明: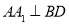 ;
;
(2)证明: 平面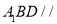 平面
平面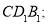
(3)求三棱柱 的体积.
的体积.
(1)详见解析;(2)详见解析;(3)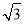 .
.
【解析】
试题分析:(1)由题意BD⊥AC ,因为A1O⊥平面ABCD可知A1O⊥BD ,可证BD⊥面A1AC即可证明结论;(2)由于A1B1∥AB ,AB∥CD,可得A1B1∥CD,又A1B1=CD,可得四边形A1B1CD是平行四边形
所以A1D∥B1C, 同理可证A1B∥CD1,利用面面平行判定定理即可证明结结论; (3) 由于A1O⊥面ABCD 故A1O是三棱柱A1B1D1-ABD的高.又在RT△A1OA中,AA1=2,AO = 1 ,可得A1O=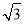 ,
,
根据柱体体积公式即可求出三棱柱ABD-A1B1D1的体积.
试题解析:(1)证明:∵底面ABCD是正方形 ∴BD⊥AC
又∵A1O⊥平面ABCD BD?面ABCD ∴A1O⊥BD
又∵A1O∩AC=O A1O?面A1AC,AC?面A1AC
∴BD⊥面A1AC AA1?面A1AC
∴AA1⊥BD 4分
(2)∵A1B1∥AB AB∥CD ∴A1B1∥CD 又A1B1=CD ∴四边形A1B1CD是平行四边形
∴A1D∥B1C 同理A1B∥CD1
∵A1B?平面A1BD, A1D ?平面A1BD, CD1?平面CD1B1, B1C?平面CD1B
且A1B∩ A1D=A1 CD1∩B1C=C
∴平面A1BD // 平面CD1B1 8分
(3) ∵A1O⊥面ABCD ∴A1O是三棱柱A1B1D1-ABD的高.
在正方形AB CD中,AO = 1 .在RT△A1OA中,AA1=2,AO = 1 ∴A1O=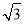
∴
所以, 三棱柱ABD-A1B1D1的体积为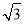 . 12分.
. 12分.
考点:1.线面垂直的判定;2.面面平行的判定;3.柱体的体积公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| A、p是真命题,¬p:?x∈R,f(x)<0 | B、p是真命题,¬p:?x0∈R,f(x0)<0 | C、p是假命题,¬p:?x∈R,f(x)≤0 | D、p是假命题,¬p:?x0∈R,f(x0)<0 |
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省五校协作体高三上学期期中考试理科数学试卷(解析版) 题型:选择题
已知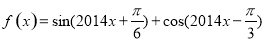 的最大值为
的最大值为 ,若存在实数
,若存在实数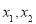 ,使得对任意实数x总有
,使得对任意实数x总有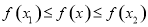 成立,则
成立,则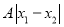 的最小值为( )
的最小值为( )
A.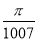 B.
B. C.
C. D.
D.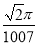
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省五校协作体高三上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
已知函数 ,
,
(1)当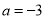 时,求不等式
时,求不等式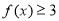 的解集;
的解集;
(2)若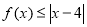 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省五校协作体高三上学期期中考试文科数学试卷(解析版) 题型:选择题
设l为直线,?,?是两个不同的平面,下列命题中正确的是( )
A.若 ,
, ,则
,则
B.若 ,
, ,则
,则
C.若 ,
, ,则
,则
D.若 ,
, ,则
,则
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检理科数学试卷(解析版) 题型:填空题
直线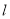 与函数
与函数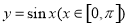 的图像相切于点
的图像相切于点 ,且
,且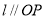 ,
, 为坐标原点,
为坐标原点,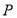 为图像的极大值点,
为图像的极大值点,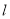 与
与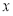 轴交于点
轴交于点 ,过切点
,过切点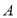 作
作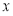 轴的垂线,垂足为
轴的垂线,垂足为 ,则
,则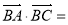 =__________.
=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com