Question

14．一个直角梯形上底、下底和高之比为$2：4：\sqrt{5}$，将此直角梯形以垂直于底的腰为轴旋转一周形成一个圆台，求这个圆台上底面积、下底面积和侧面积之比．

Answer 1

分析 由已知设直角梯形上底、下底和高为$2x，4x，\sqrt{5}x$，它们分别为圆台的上、下底半径和高，代入圆台底面积及侧面积公式，求出两底面积及侧面积，可得答案．

解答 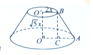解：由题意可设直角梯形上底、下底和高为$2x，4x，\sqrt{5}x$，它们分别为圆台的上、下底半径和高．
如图示，过点B作BC⊥OA于C，则Rt△ABC中，AC=OA-OC=OA-O'B=4x-2x=2x，$BC=O'O=\sqrt{5}x$，∴$AB=\sqrt{A{C^2}+B{C^2}}=\sqrt{{{（{2x}）}^2}+{{（{\sqrt{5}x}）}^2}}=3x$．
∴${S_上}：{S_下}：{S_侧}=[{π{{（{2x}）}^2}}]：[{π{{（{4x}）}^2}}]：[{π（{2x+4x}）×3x}]=2：8：9$．

点评 本题考查的知识点是旋转体，圆台的表面积，熟练掌握圆台的底面积及侧面积公式，是解答的关键．