练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】实数x，y满足 ，
    （1）若z=2x+y，求z的最大值；
    （2）若z=x2+y2 ， 求z的取值范围．

    【答案】
    （1）解：由 ，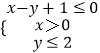

    作出可行域如图中阴影部分所示

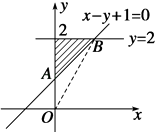
    z=2x+y令z=0画出y=﹣2x，由图知， ，可得B（1，2），

    当z=2x+y经过点B（1，2）时，zmax=4


    （2）解：z=x2+y2表示可行域内的任意一点与坐标原点之间的距离的平方．

    因此x2+y2的范围最小为|OA|2（取不到），最大为|OB|2．

    ，得A（0，1），∴|OA|2=（ ）2=1，|OB|2=（ ）2=5．

    ∴z的最大值为5，没有最小值．故z的取值范围是（1，5]


    【解析】画出约束条件的可行域，（1）利用目标函数的几何意义求解即可．（2）利用目标函数的几何意义，可行域内的点到原点的距离的平方，观察求解即可、

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，探究函数的单调性；

    （2）若关于的不等式在上恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知A，B，C为△ABC的三个内角，且其对边分别为a，b，c，若c2+b2+cb=a2
    （1）求A；
    （2）若a=2 ，b+c=4，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数

    （1）当， 恒成立，求实数的取值范围.

    （2）设在上有两个极值点.

    （A）求实数的取值范围；

    （B）求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ，（ ）.

    （1）讨论函数在上零点的个数；

    （2）若有两个不同的零点， ，求证： .

    （参考数据： 取， 取， 取）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解关于x的不等式（m+1）x2﹣4x+1≤0（m∈R）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆x2+y2=4上一定点A（2，0），B（1，1）为圆内一点，P，Q为圆上的动点．

    （1）求线段AP中点的轨迹方程；
    （2）若∠PBQ=90°，求线段PQ中点的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，正方体ABCD﹣A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′交于M、N，设BM=x，x∈[0，1]，给出以下四个命题：
    ①平面MENF⊥平面BDD′B′；
    ②当且仅当x= 时，四边形MENF的面积最小；
    ③四边形MENF周长l=f（x），x∈0，1]是单调函数；
    ④四棱锥C′﹣MENF的体积v=h（x）为常函数；
    以上命题中真命题的序号为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生，为了解学生的就业倾向，用分层抽样的方法从该校这四个专业共抽取40名学生进行调查，应在丙专业抽取的学生人数为 ．

    查看答案和解析>>

    同步练习册答案