
| 寿命(天) | 频数 | 频率 |
| [100,200) | 20 | 0.10 |
| [200,300) | 30 | a |
| [300,400) | 70 | 0.35 |
| [400,500) | b | 0.15 |
| [500,600) | 50 | 0.25 |
| 合计 | 200 | 1 |
| C | 0 3 |
| 1 |
| 4 |
| 27 |
| 64 |
| C | 1 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 27 |
| 64 |
| C | 2 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 64 |
| C | 3 3 |
| 1 |
| 4 |
| 1 |
| 64 |
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 3 |
| 4 |
| 1 |
| 4 |
| C | k 3 |
| 1 |
| 4 |
| 1 |
| 4 |


科目:高中数学 来源: 题型:
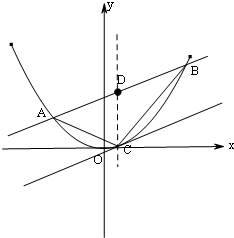 如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).查看答案和解析>>
科目:高中数学 来源: 题型:
| an+cn |
| 2 |
| an+bn |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
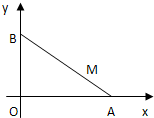 如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上的一点,且
如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上的一点,且| AM |
| MB |
| 1 |
| 2 |
| S△PQC |
| S△PQD |
| |PC| |
| |PD| |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=| π |
| 3 |
| CE |
| CC1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com