
【题目】已知函数![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的最大值 ;
上的最大值 ;
(2)若![]() 是函数
是函数![]() 图象上不同的三点,且
图象上不同的三点,且![]() ,试判断
,试判断![]() 与
与![]() 之间的大小关系,并证明 .
之间的大小关系,并证明 .
【答案】(1)见解析(2)见解析
【解析】【试题分析】求函数在某一闭区间上的最值问题,基本方法是求导,研究导数的在区间上的正负,得出函数在区间上的单调性,求极值和最值,本题关键是含有参数![]() ,所以针对
,所以针对![]() 的不同情况,进行讨论得出最值;第二步先表示出
的不同情况,进行讨论得出最值;第二步先表示出![]() 及
及![]() ,然后差值比较,重要的一个技巧是设
,然后差值比较,重要的一个技巧是设![]() ,转化为关于
,转化为关于![]() 的函数,利用导数证明不等式.
的函数,利用导数证明不等式.
(1) ![]() ,
,
当![]() 时,
时, ![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() 时,
时, ![]() ;
;
当![]() 时,由
时,由![]() ,得
,得![]() ,又
,又![]() ,则有如下分类 :
,则有如下分类 :
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上是增函数 ,所以
上是增函数 ,所以![]() ;②当
;②当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上是增函数 ,在
上是增函数 ,在![]() 上是减函数 ,所以
上是减函数 ,所以![]() ;③当
;③当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上是减函数 ,所以
上是减函数 ,所以![]() ,综上,函数
,综上,函数![]() 在
在![]() 上的最大值为
上的最大值为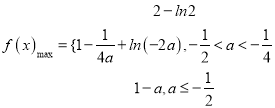 .
.
(2) ![]()
![]() ,
, ![]() ,
,
![]()
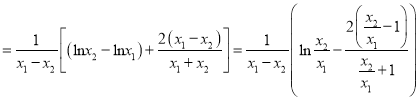 ,令
,令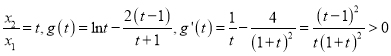 ,所以
,所以![]() 在
在![]() 上是增函数 ,又
上是增函数 ,又![]() ,当
,当![]() 时,
时, ![]() ,故
,故![]() ;当
;当![]() 时,
时, 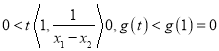 ,故
,故![]() ,综上知:
,综上知: ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知θ为向量 ![]() 与
与 ![]() 的夹角,|
的夹角,| ![]() |=2,|
|=2,| ![]() |=1,关于x的一元二次方程x2﹣|
|=1,关于x的一元二次方程x2﹣| ![]() |x+
|x+ ![]()
![]() =0有实根.
=0有实根.
(Ⅰ)求θ的取值范围;
(Ⅱ)在(Ⅰ)的条件下,求函数f(θ)=sin(2θ+ ![]() )的最值及对应的θ的值.
)的最值及对应的θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2 ![]() +
+ ![]() sinωx﹣
sinωx﹣ ![]() (ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]∪[
]∪[ ![]() ,1)
,1)
C.(0, ![]() ]
]
D.(0, ![]() ]∪[
]∪[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先将函数y=f(x)的图象向左平移 ![]() 个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)若函数y=g(x)与y=f(x)的图象关于点M( ![]() ,2)对称,求函数y=g(x)在[0,
,2)对称,求函数y=g(x)在[0, ![]() ]上的最小值和最大值.
]上的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 上的动点,
上的动点, ![]() .
.
(Ⅰ)若点![]() 是
是![]() 中点,证明:平面
中点,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)判断点![]() 到平面
到平面![]() 的距离是否为定值?若是,求出定值;若不是,请说明理由.
的距离是否为定值?若是,求出定值;若不是,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.

(1)求在未来的连续4天中,有2天的日销售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未来4天里日销售量不低于100枝的天数,求随机变量
表示在未来4天里日销售量不低于100枝的天数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一直线l过直线l1:3x﹣y=3和直线l2:x﹣2y=2的交点P,且与直线l3:x﹣y+1=0垂直.
(1)求直线l的方程;
(2)若直线l与圆心在x正半轴上的半径为 ![]() 的圆C相切,求圆C的标准方程.
的圆C相切,求圆C的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com