Question

13．从三角形内部任意一点向各边引垂线，其长度分别为d₁，d₂，d₃，且相应各边上的高分别为h₁，h₂，h₃，求证：$\frac{{d}_{1}}{{h}_{1}}$+$\frac{{d}_{2}}{{h}_{2}}$+$\frac{{d}_{3}}{{h}_{3}}$=1．类比以上性质，给出空间四面体的一个猜想，并给出证明．

Answer 1

分析 利用$\frac{{d}_{1}}{{h}_{1}}$=$\frac{\frac{1}{2}•BC•{d}_{1}}{\frac{1}{2}•BC•{h}_{1}}$=$\frac{{S}_{△MBC}}{{S}_{△ABC}}$，相加即得结论；对于空间四面体利用同底棱锥的体积等于高的比计算即得结论．

解答 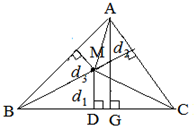证明：∵$\frac{{d}_{1}}{{h}_{1}}$=$\frac{\frac{1}{2}•BC•{d}_{1}}{\frac{1}{2}•BC•{h}_{1}}$=$\frac{{S}_{△MBC}}{{S}_{△ABC}}$，
同理，$\frac{{d}_{2}}{{h}_{2}}$=$\frac{{S}_{△MAB}}{{S}_{△ABC}}$，$\frac{{d}_{3}}{{h}_{3}}$=$\frac{{S}_{△MAC}}{{S}_{△ABC}}$，
∴$\frac{{d}_{1}}{{h}_{1}}$+$\frac{{d}_{2}}{{h}_{2}}$+$\frac{{d}_{3}}{{h}_{3}}$=$\frac{{S}_{△MBC}+{S}_{△MAB}+{S}_{△MAC}}{{S}_{△ABC}}$=1．
类比以上性质，给出空间四面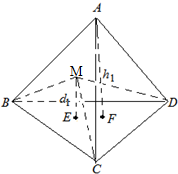体的一个猜想：
从四面体内部任意一点向各面引垂线，其长度分别为d₁，d₂，d₃，d₄，
且相应各面上的高分别为h₁，h₂，h₃，h₄，求证：$\frac{{d}_{1}}{{h}_{1}}$+$\frac{{d}_{2}}{{h}_{2}}$+$\frac{{d}_{3}}{{h}_{3}}$+$\frac{{d}_{4}}{{h}_{4}}$=1．
证明：∵$\frac{{d}_{1}}{{h}_{1}}$=$\frac{\frac{1}{3}•{S}_{△BCD}•{d}_{1}}{\frac{1}{3}•{S}_{△BCD}•{h}_{1}}$=$\frac{{V}_{M-BCD}}{{V}_{A-BCD}}$，
同理，$\frac{{d}_{2}}{{h}_{2}}$=$\frac{{V}_{M-ACD}}{{V}_{A-BCD}}$，$\frac{{d}_{3}}{{h}_{3}}$=$\frac{{V}_{M-ABD}}{{V}_{A-BCD}}$，$\frac{{d}_{4}}{{h}_{4}}$=$\frac{{V}_{M-ABC}}{{V}_{A-BCD}}$，
∴$\frac{{d}_{1}}{{h}_{1}}$+$\frac{{d}_{2}}{{h}_{2}}$+$\frac{{d}_{3}}{{h}_{3}}$+$\frac{{d}_{4}}{{h}_{4}}$=$\frac{{V}_{M-BCD}+{S}_{M-ACD}+{S}_{M-ABD}+{S}_{M-ABC}}{{V}_{A-BCD}}$=1．

点评 本题考查类比推理，涉及三角形面积公式等基础知识，注意解题方法的积累，属于基础题．