
【题目】已知函数![]() .
.
(1)求![]() 的单调递增区间.
的单调递增区间.
(2)在ΔABC中,角A,B,C所对的边分别为a,b,c,若f(A)=1,c=10,cosB=![]() ,求ΔABC的中线AD的长.
,求ΔABC的中线AD的长.
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)对定义域内的每一个值x1,在其定义域内都存在唯一的x2,使f(x1)f(x2)=1成立,则称该函数为“依赖函数”.
(1) 判断函数g(x)=2x是否为“依赖函数”,并说明理由;
(2) 若函数f(x)=(x–1)2在定义域[m,n](m>1)上为“依赖函数”,求实数m、n乘积mn的取值范围;
(3) 已知函数f(x)=(x–a)2 (a<![]() )在定义域[
)在定义域[![]() ,4]上为“依赖函数”.若存在实数x[
,4]上为“依赖函数”.若存在实数x[![]() ,4],使得对任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求实数s的最大值.
,4],使得对任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求实数s的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列语句是否为命题?如果是,判断它的真假.
(1)这道数学题有趣吗?(2)0不可能不是自然数;(3)![]() ;(4)
;(4)![]() ;
;
(5)91不是素数;(6)上海的空气质量越来越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕, ![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,检测结果如频率分布直方图所示.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,检测结果如频率分布直方图所示.
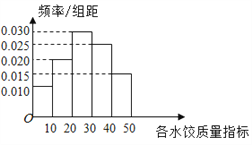
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中数据用该组区间的中点值作代表);
(同一组中数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年3月22日是第二十七届“世界水日”,3月22日-28日是第三十二届“中国水周”为了倡导“坚持节约用水”,某兴趣小组在本校4000名同学中,随机调查了40名同学家庭中一年的月均用水量(单位:吨),并将月均用水量分为6组:![]() ,[4,6),[6,8),[8,10),[10,12),[12,14]加以统计,得到如图所示的频率分布直方图.
,[4,6),[6,8),[8,10),[10,12),[12,14]加以统计,得到如图所示的频率分布直方图.

(1)求出图中实数a的值;
(2)根据样本数据,估计本校4000名同学家庭中,月均用水量低于8吨的约有多少户
(3)在月均用水量大于或等于10吨的样本数据中,该兴趣小组决定随机抽取2名同学的家庭进行回访,求这2名同学中恰有1人所在家庭的月均用水量属于[10,12)组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com