Question

【题目】问：是否存在这样的正整数数列，满足，且对每个，均有或；而其各项的值恰构成的一个排列？证明你的结论.

Answer 1

【答案】见解析

【解析】

由于，而，注意到，“差”运算具有“平移性”，即若或13，则对任意的整数，也有或13.

为此，先将集合｛1，2，…，33｝中的数排成一个圈，使得圈上任何相邻两数之差均为20或13，如图.

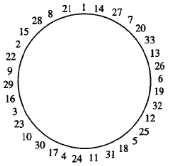
将此圈从任一间隙处剪开，铺陈的线状排列，均满足或13.

为将数列锁定，在前面添加一项，使数列也满足条件，可选择与数33相邻的一个间隙剪开.例如，从33右侧间隙剪开，并按顺时针排列就成为：

0，13，26，6，19，32，12，25，5，18，31，11，24，4，17，30，10，23，3，16，29，9，22，2，15，28，8，21，1，14，27，7，20，33，（记为）.

若从33左侧间隙剪开，并按逆时针排列则成为：

0，20，7，27，14，…，6，26，13，33.

以上两种排列均满足或13.

记分段数列，

，

其中，.

将这些段作如下联结：，所得到的数列满足条件.

事实上，，

对其中任意两个邻项、属于同一个分段，显然，或13；若相邻项、属于两个相邻段与，则是的首项，即

，

而是的末项，即，此时，.

因此，数列满足条件.