
【题目】如图,在四棱锥![]() 中,
中,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
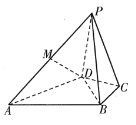
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,![]() )的最小正周期为π,且关于
)的最小正周期为π,且关于![]() 中心对称,则下列结论正确的是( )
中心对称,则下列结论正确的是( )
A.f(1)<f(0)<f(2)B.f(0)<f(2)<f(1)
C.f(2)<f(0)<f(1)D.f(2)<f(1)<f(0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,数列
,数列![]() 为
为![]() 数列,记
数列,记![]() .
.
(1)写出一个满足![]() ,且
,且![]() 的
的![]() 数列
数列![]() ;
;
(2)若![]() ,
,![]() ,证明:
,证明:![]() 数列
数列![]() 是递增数列的充要条件是
是递增数列的充要条件是![]() ;
;
(3)对任意给定的整数![]() ,是否存在首项为0的
,是否存在首项为0的![]() 数列
数列![]() ,使得
,使得![]() ?如果存在,写出一个满足条件的
?如果存在,写出一个满足条件的![]() 数列
数列![]() ;如果不存在,说明理由.
;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
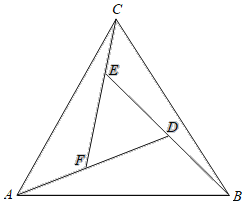
【题目】赵爽是我国汉代数学家、天文学家,他在注解《周髀算经》时,介绍了“勾股圆方图”,亦称“赵爽弦图”,它被2002年国际数学家大会选定为会徽.“赵爽弦图”是以弦为边长得到的正方形,该正方形由4个全等的直角三角形加上中间一个小正方形组成类比“赵爽弦图”,可类似地构造如图所示的图形它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形设DF=2AF=2,若在大等边三角形中随机取一点,则此点取自三个全等三角形(阴影部分)的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是我国古代计算圆周率![]() 的一种方法.在公元
的一种方法.在公元![]() 年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求
年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求![]() .当时刘微就是利用这种方法,把
.当时刘微就是利用这种方法,把![]() 的近似值计算到
的近似值计算到![]() 和
和![]() 之间,这是当时世界上对圆周率
之间,这是当时世界上对圆周率![]() 的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率
的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率![]() ,则
,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() )(参考数据
)(参考数据![]() )
)

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
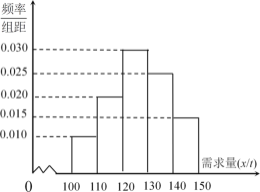
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com