练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，为正三角形，，，为线段的中点.

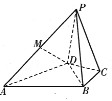
    （1）求证：平面；

    （2）若，，求直线与平面所成角的正弦值.

    【答案】（1）证明见解析（2）

    【解析】

    （1）利用中位线关系，得出//，然后再根据题意证明//，即可得出结论

    （2）先证明出平面，然后以为坐标原点，，，为轴、轴、轴建立如图所示的空间直角坐标系，然后计算出平面的法向量和，最后，利用公式求解求解即可

    （1）证明：取的中点，连接，，则//.

    又，，所以，.

    又，所以//.

    又，，

    所以平面//平面.

    又平面，

    所以//平面.

    （2）连接，，

    则为中点，，.

    又，，所以.

    又，所以平面.

    以为坐标原点，，，为轴、轴、轴建立如图所示的空间直角坐标系.

    ，，，，，

    ，，.

    设平面的法向量，

    则得.

    设直线与平面所成角为，则

    .

    故直线与平面所成角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】阿尔法狗(AlphaGo)是第一个击败人类职业围棋选手、第一个战胜围棋世界冠军的人工智能程序,由谷歌(Google)公司的团队开发.其主要工作原理是“深度学习”.2017 年5 月,在中国乌镇围棋峰会上,它与排名世界第一的世界围棋冠军柯洁对战,以3 比0 的总比分获胜.围棋界公认阿尔法围棋的棋力已经超过人类职业围棋顶尖水平.

    为了激发广大中学生对人工智能的兴趣,某市教育局组织了一次全市中学生“人工智能”软件设计竞赛,从参加比赛的学生中随机抽取了30 名学生,并把他们的比赛成绩按五个等级进行了统计,得到如下数据表:

    成绩等级

    成绩(分)

    5

    4

    3

    2

    1

    人数（名）

    4

    6

    10

    7

    3

    (1)根据上面的统计数据,试估计从本市参加比赛的学生中任意抽取一人,其成绩等级为“ 或”的

    概率;

    (2)根据(I)的结论,若从该地区参加比赛的学生(参赛人数很多)中任选3 人,记表示抽到成绩等级为“或”的学生人数,求 的分布列及其数学期望；

    (3)从这30 名学生中,随机选取2 人,求“这两个人的成绩之差大于1分”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，CM，CN为某公园景观湖胖的两条木栈道，∠MCN=120°，现拟在两条木栈道的A，B处设置观景台，记BC=a，AC=b，AB=c（单位：百米）

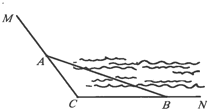
    （1）若a，b，c成等差数列，且公差为4，求b的值；

    （2）已知AB=12，记∠ABC=θ，试用θ表示观景路线A-C-B的长，并求观景路线A-C-B长的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面为矩形， 平面， 为的中点.

    （1）证明： 平面

    （2）已知， ， 求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，将边长为2的正方形沿对角线折叠，使得平面平面，又平面.

    （1）若，求直线与直线所成的角；

    （2）若二面角的大小为，求的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，为正三角形，，，，，为线段的中点．

    （1）求证：平面；

    （2）求证：平面；

    （3）求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】华为手机作为华为公司三大核心业务之一，2018年的销售量跃居全球第二名．某机构随机选取了100名华为手机的顾客进行调查，并将这100人的手机价格按照，，…，分成7组，制成如图所示的频率分布直方图．

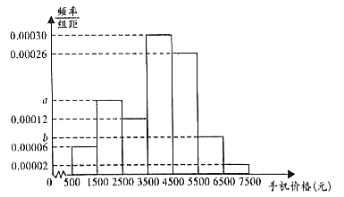
    （1）若是的2倍，求，的值；

    （2）求这100名顾客手机价格的平均数和中位数（同一组中的数据用该组区间的中间值作代表，精确到个位）；

    （3）利用分层抽样的方式从手机价格在和的顾客中选取6人，并从这6人中随机抽取2人进行回访，求抽取的2人手机价格在不同区间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，其中．

    （Ⅰ）已知函数为偶函数，求的值；

    （Ⅱ）若，证明：当时，；

    （Ⅲ）若在区间内有两个不同的零点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线的参数方程为：（为参数），的参数方程为：（为参数）.

    （1）化、的参数方程为普通方程，并说明它们分别表示什么曲线；

    （2）若直线的极坐标方程为：，曲线上的点对应的参数，曲线上的点对应的参数，求的中点到直线的距离.

    查看答案和解析>>

    同步练习册答案