练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知点在椭圆上，过点作轴于点

    （1）求线段的中点的轨迹的方程

    （2）设、两点在（1）中轨迹上，点，两直线与的斜率之积为，且（1）中轨迹上存在点满足，当面积最小时，求直线的方程．

    【答案】（1）；（2）

    【解析】

    （1）设线段的中点为，得出点的坐标为，然后代入椭圆方程并化简后得出所求轨迹方程；

    （2）设直线的方程为，设点、，将直线的方程与椭圆联立，消去，并列出韦达定理，利用直线和的斜率之积得出，可得出，由知，于是得出直线的方程为，将该直线与椭圆方程联立并结合两点间的距离公式得出，最后利用三角形的面积公式以及基本不等式求出面积的最小值，利用基本不等式等号成立的条件求出的值，即可求出直线的方程。

    （1）设线段的中点为，则，，

    即；

    （2）设直线，，，，，

    联立，得．

    ，．

    ，

    得到．

    则为，解得，同理．

    ，

    ．

    当，即时，有最小值为．

    此时直线的方程为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知抛物线，过抛物线上点B作切线交y轴于点

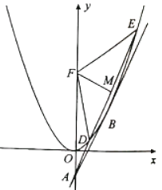
    （Ⅰ）求抛物线方程和切点的坐标；

    （Ⅱ）过点作抛物线的割线，在第一象限内的交点记为，，设为y轴上一点，满足，为中点，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知曲线的参数方程为（为参数），以直角坐标系的原点为极点，轴的正半轴为极轴，建立极坐标系，直线的极坐标方程是：

    （1）求曲线的普通方程和直线的直角坐标方程.

    （2）点是曲线上的动点，求点到直线距离的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某快递公司收取快递费用的标准是：重量不超过的包裹收费元；重量超过的包裹，除收费元之外，超过的部分，每超出（不足，按计算）需再收元.该公司将最近承揽的件包裹的重量统计如下：

    包裹重量（单位： ）

    包裹件数

    公司对近天，每天揽件数量统计如下表：

    包裹件数范围

    包裹件数

    （近似处理）

    天数

    以上数据已做近似处理，并将频率视为概率.

    （1）计算该公司未来天内恰有天揽件数在之间的概率；

    （2）（i）估计该公司对每件包裹收取的快递费的平均值；

    （ii）公司将快递费的三分之一作为前台工作人员的工资和公司利润，剩余的用作其他费用.目前前台有工作人员人，每人每天揽件不超过件，工资元.公司正在考虑是否将前台工作人员裁减人，试计算裁员前后公司每日利润的数学期望，并判断裁员是否对提高公司利润更有利？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为为参数且，，，曲线的参数方程为为参数），以为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （1）求的普通方程及的直角坐标方程；

    （2）若曲线与曲线分别交于点，，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为实常数，函数．

    （1）当时，求的单调区间；

    （2）设，不等式的解集为，不等式的解集为，当时，是否存在正整数，使得或成立．若存在，试找出所有的m；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为.

    （1）若，求直线以及曲线的直角坐标方程；

    （2）若直线与曲线交于两点，且，求直线的斜率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律，现把杨辉三角中的数从上到下，从左到右依次排列，得数列：1，1，1，1，2，1，1，3，3，1，1，4，6，4，1，…，记作数列，若数列的前项和为，则_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）讨论函数的单调性；

    （2）若函数恰有两个零点，求的取值范围.

    查看答案和解析>>

    同步练习册答案