
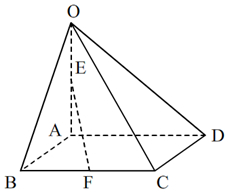
 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,分析 (1)取AD的中点G,连结EG、FG,推导出平面EFG∥平面OCD,由此能证明直线EF∥面OCD.
(2)推导出AF⊥BC,BC⊥OA,从而BC⊥面AEF,由此能证明面AEF⊥面OBC.
(3)四棱锥O-ABCD的体积V=$\frac{1}{3}×OA×{S}_{菱形ABCD}$,由此能求出结果.
解答 证明:(1)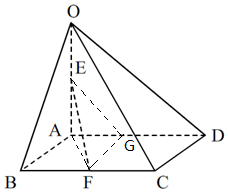 取AD的中点G,连结EG、FG,
取AD的中点G,连结EG、FG,
∵E点为OA的中点,F为BC中点,
∴FG∥CD,EG∥OD,
∵FG∩EG=G,CD∩OD=D,FG、EG?平面EFG,CD、OD?平面OCD,
∴平面EFG∥平面OCD,
∵EF?平面EFG,∴直线EF∥面OCD.
(2)∵底面ABCD是边长为2的菱形,∠ABC=60°,F为BC中点,
∴AF⊥BC,
∵OA⊥面ABCD,BC?平面ABCD,∴BC⊥OA,
∵AF∩OA=A,∴BC⊥面AEF,
∵BC?面OBC,∴面AEF⊥面OBC.
解:(3)∵底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,
∴S菱形ABCD=2×($\frac{1}{2}×2×2×sin60°$)=2$\sqrt{3}$,
故四棱锥O-ABCD的体积V=$\frac{1}{3}×OA×{S}_{菱形ABCD}$=$\frac{1}{3}×4×2\sqrt{3}$=$\frac{{8\sqrt{3}}}{3}$.
点评 本题考查线面平行、面面垂直的证明,考查几何体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:解答题
在对人们的休闲方式的一次调查中,共调查了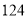 人,其中女性
人,其中女性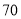 人,男性
人,男性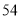 人.女性中有
人.女性中有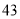 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有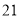 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外 人主要的休闲方式是运动.
人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)是否有97.5%的把握认为性别与休闲方式有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:填空题
已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的方差为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{3{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1 | C. | x2-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:解答题
(1)求经过直线l1:2x+3y-5=0与l2:7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程;
(2)求与直线3x+4y-7=0垂直,且与原点的距离为6的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com