
分析 求出直线l与MN平行时和直线l经过线段MN的中点时对应的直线方程,再化为一般方程即可.
解答 解:①当直线l与MN平行时,
kMN=$\frac{9-3}{4-2}$=3,
∴直线l的方程为:y-2=3(x-1),
化为一般方程为:3x-y-1=0;
②当直线l经过线段MN的中点C(3,6)时,
kPC=$\frac{6-2}{3-1}$=2,
∴直线l的方程为:y-2=2(x-1),
化为一般方程是:2x-y=0;
综上,所求的直线方程为3x-y-1=0或2x-y=0.
故答案为:3x-y-1=0或2x-y=0.
点评 本题考查了相互平行的直线斜率之间的关系、中点坐标公式、直线方程以及分类讨论方法的应用问题,是中档题.


科目:高中数学 来源: 题型:选择题
 如图所示,两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ,N为OB中点,M为OA上靠近A的三等分点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x、y∈R),则x2+y2的最小值为( )
如图所示,两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ,N为OB中点,M为OA上靠近A的三等分点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x、y∈R),则x2+y2的最小值为( )| A. | $\frac{4}{25}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
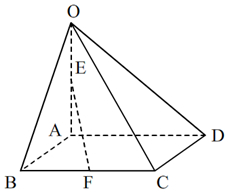 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
在直角坐标系中,已知A(-1,2),B(3,0),那么线段AB中点的坐标为( ).
A.(2,2)
B.(1,1)
C.(-2,-2)
D.(-1,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com