
分析 (Ⅰ)先把曲线C的参数方程化为直角坐标方程,由此能求出曲线C的极坐标方程.
(Ⅱ)求出直线l的直角坐标方程为y=tanα•x,圆心C(0,3)到直线的距离d=$\frac{|3|}{\sqrt{1+ta{n}^{2}α}}$,再由$|AB|=2\sqrt{3}$,利用勾股定理求出tan2α=$\frac{7}{2}$,由此能求出直线l的斜率.
解答 解:(Ⅰ)∵曲线C的参数方程为:$\left\{\begin{array}{l}x=\sqrt{5}cosθ\\ y=3+\sqrt{5}sinθ\end{array}\right.$(其中θ为参数),
∴曲线C的直角坐标方程为x2+(y-3)2=5,即x2+y2-6y+4=0,
∴曲线C的极坐标方程为ρ2-6ρsinθ+4=0.
(Ⅱ)∵直线l的参数方程为:$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$(其中t为参数),
∴直线l的直角坐标方程为y=tanα•x,
圆心C(0,3)到直线的距离d=$\frac{|3|}{\sqrt{1+ta{n}^{2}α}}$,
∵直线l与曲线C分别交于A,B两点,且$|AB|=2\sqrt{3}$,
∴$\sqrt{{r}^{2}-{d}^{2}}=\frac{|AB|}{2}$,
即$\sqrt{5-\frac{9}{1+ta{n}^{2}α}}$=$\sqrt{3}$,解得tan2α=$\frac{7}{2}$,
∴tanα=±$\frac{\sqrt{14}}{2}$.
∴直线l的斜率为$±\frac{\sqrt{14}}{2}$.
点评 本题考查圆、直线方程、极坐标方程、直角坐标方程、参数方程、点到直线距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A(x-x0)+B(y-y0)=0 | B. | B(x-x0)+A(y-y0)=0 | C. | A(x-x0)-B(y-y0)=0 | D. | B(x-x0)-A(y-y0)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
下列说法错误的是( )
A.若直线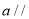 平面
平面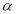 ,直线
,直线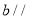 平面
平面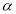 ,则直线
,则直线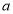 不一定平行于直线
不一定平行于直线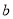
B.若平面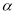 不垂直于平面
不垂直于平面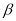 ,则
,则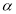 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面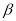
C.若平面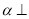 平面
平面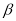 ,则
,则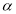 内一定不存在直线平行于平面
内一定不存在直线平行于平面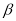
D.若平面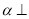 平面
平面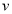 ,平面
,平面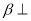 平面
平面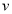 ,
,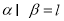 ,则
,则 一定垂直于平面
一定垂直于平面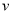
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com