
| A. | A(x-x0)+B(y-y0)=0 | B. | B(x-x0)+A(y-y0)=0 | C. | A(x-x0)-B(y-y0)=0 | D. | B(x-x0)-A(y-y0)=0 |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:填空题
已知直线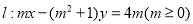 和圆
和圆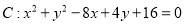 .有以下几个结论:
.有以下几个结论:
①直线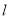 的倾斜角不是钝角;
的倾斜角不是钝角;
②直线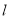 必过第一、三、四象限;
必过第一、三、四象限;
③直线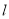 能将圆
能将圆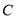 分割成弧长的比值为
分割成弧长的比值为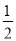 的两段圆弧;
的两段圆弧;
④直线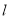 与圆
与圆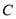 相交的最大弦长为
相交的最大弦长为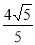 .
.
其中正确的是________________.(写出所有正确说法的番号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com