
分析 (1)根据正弦定理及两角和的正弦公式,求得sinB=2sinBcosC,求得cosC=$\frac{1}{2}$,根据C的取值范围,即可求得角C的大小;
(2)由余弦定理求得c=2$\sqrt{7}$,设CD=x,在△ABC和△ACD中,分别应用余弦定理求得cosA=$\frac{2}{\sqrt{7}}$,cosA=$\frac{3}{x}$,联立即可求得CD的长.
解答  解:(1)由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,(R为外接圆半径),
解:(1)由正弦定理可知:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,(R为外接圆半径),
a=2RsinA,b=2RsinB,c=2RsinC,
由2ccosB+b=2a,2sinCcosB+sinB=2sinA=2sin(B+C)=2sinBcosC+2cosBsinC,
∴sinB=2sinBcosC,由B∈(0,π),则sinB≠0,
则cosC=$\frac{1}{2}$,
由C∈(0,π),
则C=$\frac{π}{3}$,
∴角C为$\frac{π}{3}$;
(2)由余弦定理得:c2=a2+b2-2abcosC=28,则c=2$\sqrt{7}$,
设CD=x,则在△ABC中,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{36+28-16}{2×6×2\sqrt{7}}$=$\frac{2}{\sqrt{7}}$,
在△ACD中,cosA=$\frac{36+{x}^{2}-{x}^{2}}{2•6•x}$=$\frac{3}{x}$,
∴$\frac{2}{\sqrt{7}}$=$\frac{3}{x}$,解得:x=$\frac{3\sqrt{7}}{2}$,
∴CD的长$\frac{3\sqrt{7}}{2}$.
点评 本题考查正弦定理及余弦定理的应用,考查两角和的正弦公式,考查计算能力,属于中档题.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 14 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A(x-x0)+B(y-y0)=0 | B. | B(x-x0)+A(y-y0)=0 | C. | A(x-x0)-B(y-y0)=0 | D. | B(x-x0)-A(y-y0)=0 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:填空题
已知一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,则这组数据的方差为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川省高二上学期期中考数学试卷(解析版) 题型:选择题
已知恒过定点(1,1)的圆C截直线 所得弦长为2,则圆心C的轨迹方程为( )
所得弦长为2,则圆心C的轨迹方程为( )
A.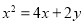 B.
B.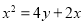
C.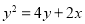 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com