
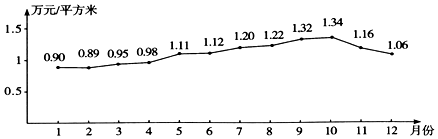
���� ��1�������⣬����$\overline{x}$��$\overline{y}$������ع�ϵ��$\stackrel{��}{b}$��$\stackrel{��}{a}$������д���ع鷽�̣�
��2�����ã�1���лع鷽�̣�����x=12ʱ$\stackrel{��}{y}$��ֵ���ɣ�
��� �⣺��1�������⣬�ó��±���
| �·�x | 3 | 4 | 5 | 6 | 7 |
| ����y | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 |
���� ���⿼���˻ع�ֱ�߷��̵�����Ӧ�����⣬��ȷ�����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{8}{9}$ | B�� | $\frac{7}{5}$ | C�� | $\frac{2}{5}$ | D�� | $\frac{8}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
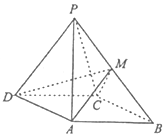 ��ͼ������P-ABCD�У�����PDC���������Σ�����ABCD�DZ߳�Ϊ2$\sqrt{3}$�����Σ���DAB=120�㣬�Ҳ���PDC����洹ֱ��MΪPB���е㣮
��ͼ������P-ABCD�У�����PDC���������Σ�����ABCD�DZ߳�Ϊ2$\sqrt{3}$�����Σ���DAB=120�㣬�Ҳ���PDC����洹ֱ��MΪPB���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com