练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知正数a，b满足a2+ab-3=0，则4a+b的最小值为6．

    分析 正数a，b满足a2+ab-3=0，可得3a•（a+b）=9．变形4a+b=3a+（a+b），利用基本不等式的性质即可得出．

    解答 解：∵正数a，b满足a2+ab-3=0，∴3a•（a+b）=9．
    则4a+b=3a+（a+b）≥2$\sqrt{3a•（a+b）}$=2$\sqrt{9}$=6，当且仅当3a=a+b，a2+ab-3=0，即b=2a=2时取等号．
    则4a+b的最小值为为6．
    故答案为：6．

    点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．如图所示，两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ，N为OB中点，M为OA上靠近A的三等分点，点C在直线MN上，且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$（x、y∈R），则x2+y2的最小值为（　　）
    A．$\frac{4}{25}$B．$\frac{2}{5}$C．$\frac{4}{9}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在△ABC中，角A，B，C的对边分别为a，b，c，已知2ccosB+b=2a，b=6，a=4．
    （1）求角C的大小；
    （2）若点D在AB边上，AD=CD，求CD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．在△ABC中，内角A，B，C所对的边长分别为a，b，c．asinBcosC+csinBcosA=$\frac{1}{2}$b且a＞b，则∠B=（　　）
    A．$\frac{5π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知abcd≠0，则“a，b，c，d成等比数列”是“ad=bc”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若不等式|x-1|+|x+m|≤4的解集非空，则实数m的取值范围是（　　）
    A．[-5，-3]B．[-3，5]C．[-5，3]D．[3，5]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

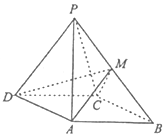    5．如图，四棱锥P-ABCD中，侧面PDC是正三角形，底面ABCD是边长为2$\sqrt{3}$的菱形，∠DAB=120°，且侧面PDC与底面垂直，M为PB的中点．
    （Ⅰ）求证：PA⊥平面CDM
    （Ⅱ）求二面角D-MC-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源：2016-2017学年河北省高二理上第一次月考数学试卷（解析版） 题型：选择题

    在直角坐标系中，已知A（－1，2），B（3，0），那么线段AB中点的坐标为（ ）．

    A．（2，2）

    B．（1，1）

    C．（－2，－2）

    D．（－1，－1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图时，若输入a，b分别为18，27，则输出的a=（　　）
    A．0B．9C．18D．54

    查看答案和解析>>

    同步练习册答案