
【题目】如图有一景区的平面图是一半圆形,其中直径长为![]() 两点在半圆弧上满足
两点在半圆弧上满足![]() ,设
,设![]() ,现要在景区内铺设一条观光通道,由
,现要在景区内铺设一条观光通道,由![]() 和
和 ![]() 组成.
组成.
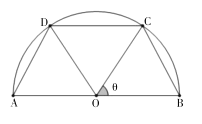
(1)用![]() 表示观光通道的长
表示观光通道的长![]() ,并求观光通道
,并求观光通道![]() 的最大值;
的最大值;
(2)现要在景区内绿化,其中在![]() 中种植鲜花,在
中种植鲜花,在![]() 中种植果树,在扇形
中种植果树,在扇形![]() 内种植草坪,已知单位面积内种植鲜花和种植果树的利润均是种植草坪利润的
内种植草坪,已知单位面积内种植鲜花和种植果树的利润均是种植草坪利润的![]() 倍,则当
倍,则当![]() 为何值时总利润最大?
为何值时总利润最大?
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知F为椭圆C:![]() 的左焦点,过F作两条互相垂直的直线
的左焦点,过F作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与C交于A,B两点,直线
与C交于A,B两点,直线![]() 与C交于D,E两点,则四边形ADBE的面积最小值为( )
与C交于D,E两点,则四边形ADBE的面积最小值为( )
A.4B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们在求高次方程或超越方程的近似解时常用二分法求解,在实际生活中还有三分法.比如借助天平鉴别假币.有三枚形状大小完全相同的硬币,其中有一假币(质量较轻),把两枚硬币放在天平的两端,若天平平衡,则剩余一枚为假币,若天平不平衡,较轻的一端放的硬币为假币.现有 27 枚这样的硬币,其中有一枚是假币(质量较轻),如果只有一台天平,则一定能找到这枚假币所需要使用天平的最少次数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心C在直线![]() 上,且与x轴正半轴相切,点C与坐标原点O的距离为
上,且与x轴正半轴相切,点C与坐标原点O的距离为![]() .
.
(1)求圆C的标准方程;
(2)直线l过点 ![]() 且与圆C相交于A,B两点,求弦长
且与圆C相交于A,B两点,求弦长![]() 的最小值及此时直线l的方程.
的最小值及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com