
已知函数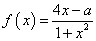 在区间
在区间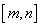 上为增函数,且
上为增函数,且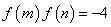 。
。
(1)当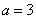 时,求
时,求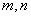 的值;(2)当
的值;(2)当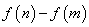 最小时,①求
最小时,①求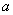 的值; ②若
的值; ②若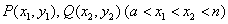 是
是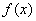 图象上的两点,且存在实数
图象上的两点,且存在实数 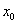 使得
使得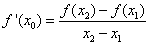 ,证明:
,证明: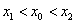 。
。
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
观察下列事实|x|+|y|=1的不同整数解(x,y)的个数为4 , |x|+|y|=2的不同整数解(x,y)的个数为8, |x|+|y|=3的不同整数解(x,y)的个数为12 .则|x|+|y|=20的不同整数解(x,y)的个数为 ( )A.76 B.80 C.86 D.92
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的前n项和为Sn,令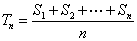 ,称Tn为数列a1,a2,…,an的“理想数”.已知a1,a2,…,a500的“理想数”为1002,那么数列3,a1,a2,….a500的“理想数”为 ( ) A.1001 B.1003 C.1004 D.1005
,称Tn为数列a1,a2,…,an的“理想数”.已知a1,a2,…,a500的“理想数”为1002,那么数列3,a1,a2,….a500的“理想数”为 ( ) A.1001 B.1003 C.1004 D.1005
查看答案和解析>>
科目:高中数学 来源: 题型:
若数列{an}是等差数列,公差为d且d≠0,a1、d∈R,{an}的前n项和记为Sn,设集合P={(x,y)|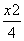 -y2=1,x、y∈R},Q={(x,y)|x=an,y=
-y2=1,x、y∈R},Q={(x,y)|x=an,y=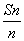 ,n∈N*},给出下列命题:
,n∈N*},给出下列命题:
①集合Q表示的图形是一条直线;②P∩Q=∅;③P∩Q只有一个元素;④P∩Q至多有一个元素.
其中正确的命题序号是________.(注:把你认为是正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com