
设x,y满足约束条件 ,
,
(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求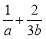 的最小值.
的最小值.
(1)10;(2)4
【解析】
试题分析:(1)如图

先在直角坐标系中画出各直线方程,再用特殊点代入法判断各不等式表示的平面区域,其公共部分即为不等式组表示的平面区域,用分割法即可求出其面积。(2)画出目标函数线,平移使其经过可行域当目标函数线的纵截距最大时, 取得最大值,求出满足条件的此点坐标代入目标函数。用基本不等式求
取得最大值,求出满足条件的此点坐标代入目标函数。用基本不等式求 的最小值。
的最小值。
试题解析:【解析】
(1)不等式表示的平面区域如图所示阴影部分. 3分
联立 得点C坐标为(4,6)
得点C坐标为(4,6)
平面区域的面积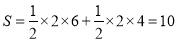 . 6分
. 6分
(2)当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线3x-y-6=0的交点C(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大值4,即4a+6b=4,
即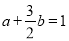 . 9分
. 9分
所以
等号成立当且仅当 时取到.
时取到.
故 的最小值为4. 12分
的最小值为4. 12分
考点:1线性规划;2基本不等式。


科目:高中数学 来源:2015届山东威海高二上学期期末考试文科数学试卷(解析版) 题型:选择题
若 ,则“
,则“ ”是方程“
”是方程“ ”表示双曲线的( )
”表示双曲线的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届安徽蚌埠高二第一学期期末考试理科数学试卷(解析版) 题型:填空题
如果圆x2+y2-2ax-2ay+2a2-4=0与圆x2+y2=4总相交,则实数a的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源:2015届安徽蚌埠高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
如图,正三棱锥S—ABC中,∠BSC=40°,SB=2,一质点从点B出发,沿着三棱锥的侧面绕行一周回到点B的最短路线的长为( )
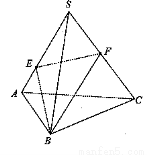
A.2 B.3 C.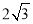 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届安徽蚌埠高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°,E为PC的中点,则异面直线PA与BE所成角为( )
A.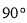 B.
B.
 C.
C.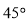 D.
D.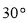
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com