Question

【题目】某个服装店经营某种服装，在某周内获纯利y(元)与该周每天销售这些服装件数x之间有如下一组数据：

x	3	4	5	6	7	8	9
y	66	69	73	81	89	90	91

已知＝280， yi＝3 487，

(1)求；

(2)求纯利y与每天销售件数x之间的回归直线方程；

(3)每天多销售1件，纯利y增加多少元？

Answer 1

【答案】（1）6,79.86；（2）＝51.36＋4.75x，（3）每天多销售1件，纯利平均增加4.75元．

【解析】试题分析：（1）根据平均数的公式，即可求得的值；

（2）利用回归系数的计算公式，求解，代入，求得，即可得到回归方程；

（3）利用回归直线方程，即可作出每天多销售1件，纯利平均增加值，作出预测．

试题解析：

(1)＝ (3＋4＋5＋…＋9)＝6，

＝ (66＋69＋…＋91)≈79.86.

(2)设回归直线方程为＝＋x，

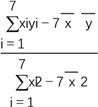则＝＝≈4.75.

＝－≈79.86－4.75×6＝51.36.

∴所求的回归直线方程为＝51.36＋4.75x.

（3）每天多销售1件，纯利平均增加4.75元．