
分析 根据题意,首先由等可能事件的概率公式计算每次抛掷两颗骰子点数和大于6的概率,由对立事件的概率性质,可得点数和小于等于6的概率;分别求出先投掷的人第一轮获胜、第二轮获胜…的概率,分析可得P1、P2、P3、…Pn、…,组成以$\frac{7}{12}$首项,($\frac{5}{12}$)2为公比的无穷等比数列,由等比数列的前n项和公式,结合极限计算方法,计算可得答案.
解答 解:根据题意,一次投掷两颗,每颗骰子有6种情况,共有6×6=36种情况,
而点数之和大于6的情况有21种,则每次抛掷两颗骰子点数和大于6的概率为$\frac{21}{36}$=$\frac{7}{12}$,
则抛掷每次两颗骰子点数和小于等于6的概率为1-$\frac{7}{12}$=$\frac{5}{12}$;
若先投掷的人第一轮获胜,其概率为P1=$\frac{7}{12}$,
若先投掷的人第二轮获胜,即第一轮两人的点数之和都小于或等于6,则其概率为P2=($\frac{5}{12}$)2×$\frac{7}{12}$,
若先投掷的人第三轮获胜,即前两轮两人的点数之和都小于或等于6,则其概率为P3=($\frac{5}{12}$)4×$\frac{7}{12}$,
若先投掷的人第四轮获胜,即前三轮两人的点数之和都小于或等于6,则其概率为P3=($\frac{5}{12}$)6×$\frac{7}{12}$,
…
分析可得,若先投掷的人第n轮获胜,其概率为Pn=($\frac{5}{12}$)2n-2×$\frac{7}{12}$,
P1、P2、P3、…Pn、…,组成以$\frac{7}{12}$首项,($\frac{5}{12}$)2为公比的无穷等比数列,
则先投掷的人获胜的概率由极限的性质,可得P1+P2+P3+…+Pn+…=$\frac{\frac{7}{12}}{1-(\frac{5}{12})^{2}}$=$\frac{12}{17}$.
故答案为$\frac{12}{17}$.
点评 本题考查等可能事件的概率的计算,涉及等比数列的前n项和与极限的计算;关键是分类分析、计算先投掷的人获胜的情况,进而由等比数列前n项公式计算.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{2}$ | C. | $\frac{17}{24}$ | D. | -$\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
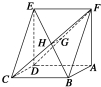 如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
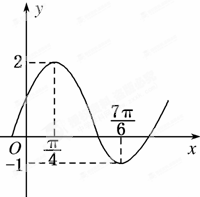 将函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,0<φ<π)的图象向右平移$\frac{2π}{3}$个单位,所得曲线的一部分如图所示,则f(x)的解析式为( )
将函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,0<φ<π)的图象向右平移$\frac{2π}{3}$个单位,所得曲线的一部分如图所示,则f(x)的解析式为( )| A. | f(x)=$\frac{3}{2}$sin($\frac{12}{11}$x-$\frac{21π}{22}$)+1 | B. | f(x)=$\frac{3}{2}$sin($\frac{12}{11}$x+$\frac{21π}{22}$)+$\frac{1}{2}$ | ||
| C. | f(x)=2sin($\frac{11}{12}$x+$\frac{21π}{22}$)-$\frac{1}{2}$ | D. | f(x)=$\frac{3}{2}$sin($\frac{12}{11}$x+$\frac{5π}{22}$)+$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
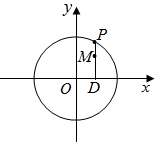 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com