练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设直线l：x-y+m=0与抛物线C：y2=4x交于不同两点A、B，F为抛物线的焦点，则△ABF的重心G的轨迹的普通方程为
     
    ．
    考点：轨迹方程
    专题：计算题,圆锥曲线的定义、性质与方程
    分析：设出A、B、G的坐标，联立直线与抛物线，利用重心坐标公式，即可求得重心G的轨迹方程．
    解答： 解：设A（x1，y1），B（x2，y2），F（1，0），重心G（x，y），
    联立直线与抛物线，消元可得y2-4y+4m=0
    ∴△＞0⇒m＜1且m≠-1（因为A、B、F不共线）
    故x=
    x2+x2+1
    3
    =
    y1+y2-2m+1
    3
    =
    5-2m
    3
    ，y=
    y1+y2
    3
    =
    4
    3

    ∴重心G的轨迹方程为y=
    4
    3
    (x＞1且x≠
    7
    3
    )    ．
    故答案为：y=
    4
    3
    (x＞1且x≠
    7
    3
    )    ．
    点评：本题考查轨迹方程，考查学生的计算能力，比较基础．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

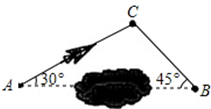    一架飞机从马来西亚吉隆坡飞往中国北京，两地相距4500km．飞行员为了避开某一区域的雷雨云层，从机场起飞以后，就沿与原来的飞行方向成30°角的方向飞行，飞行到途中，再沿与原来的飞行方向成45°角的方向继续飞行直到终点．这样飞机的飞行路程比原来的路程4500km远了多少？（参考数据：
    		3
    ≈1.73，
    		2
    ≈1.41，要求在结果完全化简后再代入参考数据运算，结果保留整数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对称轴都在坐标轴上的等轴双曲线的一个焦点是（-6，0），则它的标准方程是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=（sinx+cosx）2-2sin2x-m在[0，
    π
    2
    ]上有两个零点，则实数m的取值范围是（　　）
    A、[1，
    		2
    ）
    B、[1，
    		2
    ]
    C、（1，
    		2
    ）
    D、[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，若|
    AB
    |=2，|
    AC
    |=3，
    AB
    •
    AC
    =-3，则S△ABC=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}中，a1=1，a4=-55，且数列{an+1}为等比数列，则a2=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于函数f（x），使f（x）成立的所有常数（-∞，0）中，我们把f（x）的最小值[0，+∞）叫做函数
    g（x）的上确界．则函数f（0）=1的上确界是（　　）
    A、0
    B、
    1
    2
    C、1
    D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在R上的函数f（x）满足f（x）=
    log2(4-x)，x≤0
    f(x-1)-f(x-2)，x＞0
    ，则f（2013）的值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）+2f（
    1
    x
    ）=3x．
    （1）求f（x）的解析式，并标注定义域；
    （2）指出f（x）的单调区间，并用定义加以证明．

    查看答案和解析>>

    同步练习册答案