
在平面直角坐标系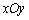 中,椭圆
中,椭圆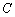 的参数方程为
的参数方程为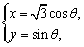 其中
其中 为参数.以
为参数.以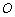 为
为
极点,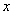 轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
轴正半轴为极轴建立极坐标系,直线l的极坐标方程为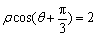 .求
.求
椭圆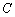 上的点到直线l距离的最大值和最小值.
上的点到直线l距离的最大值和最小值.
科目:高中数学 来源: 题型:
假设在6分钟内的任意时刻,两架相同型号的飞机机会均等地进入同一飞机场,若这两架飞机进入机场的时间之差不小于2分钟,飞机不会受到干扰;则飞机受到干扰的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列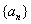 的各项均为正数,若对任意的
的各项均为正数,若对任意的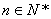 ,存在
,存在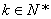 ,
,
使得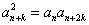 成立,则称数列
成立,则称数列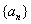 为“
为“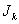 型”数列.
型”数列.
(1)若数列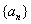 是“
是“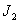 型”数列,且
型”数列,且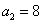 ,
,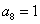 ,求
,求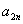 ;
;
(2)若数列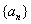 既是“
既是“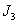 型”数列,又是“
型”数列,又是“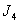 型”数列,证明数列
型”数列,证明数列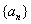 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
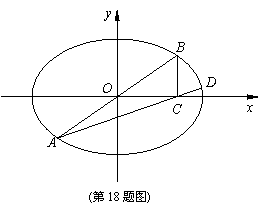
在平面直角坐标系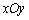 中,已知椭圆
中,已知椭圆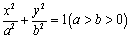 与直线
与直线 相交于
相交于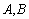 两点(从左至右),过点
两点(从左至右),过点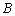 作
作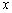 轴的垂线,垂足为
轴的垂线,垂足为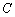 ,直线
,直线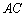 交椭圆于另一点
交椭圆于另一点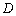 .
.
(1)若椭圆的离心率为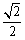 ,点
,点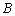 的坐标为
的坐标为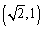 ,求椭圆的方程;
,求椭圆的方程;
 (2)若以
(2)若以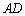 为直径的圆恰好经过点
为直径的圆恰好经过点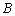 ,求椭圆的离心率.
,求椭圆的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
设P1,P2,…,Pj为集合P={1,2,…,i}的子集,其中i,j为正整数.记aij为满足P1∩P2∩…∩Pj=的有序子集组(P1,P2,…,Pj)的个数.
(1)求a22的值;
(2)求aij的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,角A,B,C的对边分别是a,b,c,满足b2+c2=bc+a2.
(1)求角A的大小;
(2)已知等差数列{an}的公差不为零,若a1cosA=1,且a2,a4, a8成等比数列,求{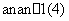 }的前n项和Sn.
}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com