
已知向量
 ,函数
,函数
(1)求函数 的最小正周期;
的最小正周期;
(2)已知 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边, ,且
,且 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
已知ΔABC中,满足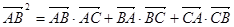 ,a,b,c分别是ΔABC的三边。
,a,b,c分别是ΔABC的三边。
(1)试判定ΔABC的形状,并求sinA+sinB的取值范围。
(2)若不等式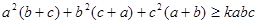 对任意的a,b,c都成立,求实数k的取值范围。
对任意的a,b,c都成立,求实数k的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
风景秀美的京娘湖畔有四棵高大的银杏树,记做 、
、 、
、 、
、 ,欲测量
,欲测量 、
、 两棵树和
两棵树和 、
、 两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得
两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得 、
、 两点间的距离为
两点间的距离为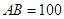 米,如图,同时也能测量出
米,如图,同时也能测量出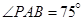 ,
, ,
, ,
,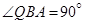 ,则
,则 、
、 两棵树和
两棵树和 、
、 两棵树之间的距离各为多少?
两棵树之间的距离各为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知锐角△ABC的三内角A、B、C的对边分别是a、b、c, 且(b2+c2-a2)tanA= bc.
bc.
(1)求角A的大小;
(2)求sin(A+10°)·[1- tan(A-10°)]的值.
tan(A-10°)]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com