
【题目】求下列函数的值域:
(1)y=![]() ;
;
(2)y=![]() ;
;
(3)y=x+4![]() ;
;
(4)y=![]() (x>1)
(x>1)
【答案】(1) {y|y≠3};(2) (0,5];(3) (-∞,5];(4) [4,+∞).
【解析】
(1)根据分式函数的性质,利用分子常数化进行求解.(2)分母进行配方,利用一元二次函数以及分式函数的性质进行求解,(3)利用换元法转化为一元二次函数进行求解.(4)利用分式的性质,结合基本不等式的应用进行求解.
(1)y![]() 3
3![]() ,则y≠3,
,则y≠3,
即函数的值域为{y|y≠3};
(2)y![]() ,
,
∵2(x﹣1)2+1≥1,∴![]() ∈(0,5],即函数的值域为(0,5];
∈(0,5],即函数的值域为(0,5];
(3)由1﹣x≥0得x≤1,则函数的定义域为(﹣∞,1],
设t![]() ,则x=1﹣t2,t≥0,
,则x=1﹣t2,t≥0,
则y=x+4![]() 1﹣t2+4t=﹣(t﹣2)2+5,
1﹣t2+4t=﹣(t﹣2)2+5,
∵t≥0,∴y≤5,即函数的值域为(﹣∞,5]
(4)y![]() x﹣1
x﹣1![]() 2,
2,
∵x>1,∴x﹣1>0,
则y=x﹣1![]() 2≥2+2
2≥2+2![]() 2+2=4,
2+2=4,
当且仅当x﹣1![]() ,解集x﹣1=1,x=2时,取等号,
,解集x﹣1=1,x=2时,取等号,
故函数的值域为[4,+∞).


科目:高中数学 来源: 题型:
【题目】某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:

(1)根据以上两个直方图完成下面的![]() 列联表:
列联表:
性别 成绩 | 优秀 | 不优秀 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
附:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P在圆柱OO1的底面⊙O上,![]() 分别为⊙O、⊙O1的直径,且
分别为⊙O、⊙O1的直径,且![]() 平面
平面![]() .
.
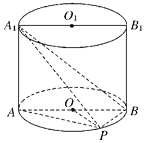
(1)求证:![]() ;
;
(2)若圆柱![]() 的体积
的体积![]() ,
,
①求三棱锥A1﹣APB的体积.
②在线段AP上是否存在一点M,使异面直线OM与![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈R,|x|<1时,有如下表达式:1+x+x2+…+xn+…= ![]()
两边同时积分得: ![]() dx+
dx+ ![]() xdx+
xdx+ ![]() x2dx+…+
x2dx+…+ ![]() xndx+…=
xndx+…= ![]()
![]() dx
dx
从而得到如下等式:1× ![]() +
+ ![]() ×(
×( ![]() )2+
)2+ ![]() ×(
×( ![]() )3+…+
)3+…+ ![]() ×(
×( ![]() )n+1+…=ln2
)n+1+…=ln2
请根据以上材料所蕴含的数学思想方法,计算:![]() ×
× ![]() +
+ ![]()
![]() ×(
×( ![]() )2+
)2+ ![]()
![]() ×(
×( ![]() )3+…+
)3+…+ ![]()
![]() ×(
×( ![]() )n+1= .
)n+1= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某种书籍的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.


表中![]() .
.
为了预测印刷20千册时每册的成本费,建立了两个回归模型:![]() .
.
(1)根据散点图,拟认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷20千册时每册的成本费.
的回归方程,并预测印刷20千册时每册的成本费.
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①用 刻画回归效果,当
刻画回归效果,当![]() 越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程
越大时,模型的拟合效果越差,反之则越好;②归纳推理是由特殊到一般的推理,而演绎推移则是由一般到特殊的推理;③综合法证明数学问题是“由因索果”,分析法证明数学问题是“执果索因”;④设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位;⑤线性回归方程
平均增加5个单位;⑤线性回归方程![]() 必过点
必过点![]() .其中错误的个数有( )
.其中错误的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() 的焦点在x轴上
的焦点在x轴上
(1)若椭圆E的焦距为1,求椭圆E的方程;
(2)设F1 , F2分别是椭圆E的左、右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q,证明:当a变化时,点P在某定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com