
����Ŀ����������˵�������� �̻��ع�Ч������
�̻��ع�Ч������![]() Խ��ʱ��ģ�͵����Ч��Խ���֮��Խ�ã��ڹ��������������һ�������������������������һ�㵽��������������ۺϷ�֤����ѧ�����ǡ�������������������֤����ѧ�����ǡ�ִ������������һ���ع鷽��
Խ��ʱ��ģ�͵����Ч��Խ���֮��Խ�ã��ڹ��������������һ�������������������������һ�㵽��������������ۺϷ�֤����ѧ�����ǡ�������������������֤����ѧ�����ǡ�ִ������������һ���ع鷽��![]() ������
������![]() ����1����λʱ��
����1����λʱ��![]() ƽ������5����λ�������Իع鷽��
ƽ������5����λ�������Իع鷽��![]() �ع���
�ع���![]() .���д���ĸ����У� ��
.���д���ĸ����У� ��
A. 0�� B. 1�� C. 2�� D. 3��
���𰸡�B
���������������ٿ������ָ���ĸ����ж�;�ڢ�������,�ۺϷ��ͷ�֤���ĸ����жϣ��ܺ͢������Իع�����жϼ���.
��⣺�����ָ��![]() Խ��,�������Խǿ,ģ�͵����Ч��Խ��.����;
Խ��,�������Խǿ,ģ�͵����Ч��Խ��.����;
�� ���������������һ�������,��������������һ�㵽���������,�ɹ������������������ĸ����֪��ȷ.
���ۺϷ�֤����ѧ�����ǡ�����������,������֤����ѧ�����ǡ�ִ������,�ɸ����֪��ȷ.
���ɻع鷽�̵�ϵ������֪��������![]() ����1����λʱ��
����1����λʱ��![]() ƽ������5����λ����ȷ��
ƽ������5����λ����ȷ��
�����Իع鷽��![]() �ع��������ĵ�
�ع��������ĵ�![]() ����ȷ.
����ȷ.
��ѡB.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
����������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
����������![]() ������
������![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�����躯��![]() ������
������![]() .֤����
.֤����![]() ��ͼ����
��ͼ����![]() ͼ����·�.
ͼ����·�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij���鼮ÿ��ijɱ���![]() ��Ԫ����ӡˢ����
��Ԫ����ӡˢ����![]() ��ǧ�ᣩ���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.
��ǧ�ᣩ���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.

|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
����![]() ��
��![]() .
.
Ϊ��Ԥ��ӡˢ20ǧ��ʱÿ��ijɱ��ѣ������������ع�ģ�ͣ�![]() ��
��![]() .
.
��1������ɢ��ͼ������Ϊѡ���ĸ�ģ��Ԥ����ɿ�����ֻѡ��ģ�ͼ��ɣ�
��2�������������ݺͣ�1����ѡ���ģ�ͣ���![]() ����
����![]() �Ļع鷽�̣���Ԥ��ӡˢ20ǧ��ʱÿ��ijɱ���.
�Ļع鷽�̣���Ԥ��ӡˢ20ǧ��ʱÿ��ijɱ���.
��������һ������![]() ��
��![]() ������
������![]() ����ع鷽��
����ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ�� ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ͱ��ս������һ���罻�����Ϸ���Ĵ��ƹ�������涨����������Ҫô��24Сʱ�ڽ�����ս��Ҫôѡ��Ϊ���ƻ�������������ս�������Ҳ����ظ��μӸû.���������߽�����ս���������������Ϸ����Լ�����ˮ����ȫ������Ƶ���ݣ�Ȼ��������������3���˲�������.����ÿ���˽�����ս�Ͳ�������ս�ǵȿ��ܵģ��һ���Ӱ��.
��1����ij�����߽�����ս������3���˷������룬����3������������2���˽�����ս�ĸ����Ƕ��٣�
��2��Ϊ�˽��Ͱ��ս���������ߵ��Ա��Ƿ��йأ�ij�����������������������飬����õ�����![]() ��������
��������
�Ա� �ɼ� | ������ս | ��������ս | �ܼ� |
���� | 45 | 15 | 60 |
�� | 25 | 15 | 40 |
�ܼ� | 70 | 30 | 100 |
���ݱ������ݣ�������90%�İ�����Ϊ����Ͱ��ս���������ߵ��Ա��йء���
����![]() ������
������![]() .
.
| 2.706 | 3.841 | 6.635 | 10.828 |
| 0.10 | 0.05 | 0.010 | 0.001 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ��������
��������![]() ����
����![]() ����
����![]() ������
������![]() ����
����![]() ����ǰ9���Ϊ63��
����ǰ9���Ϊ63��
��1��������![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ������
������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����������������
����������������![]() ������
������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������![]() ���������
���������![]() Ϊ����ʱ��
Ϊ����ʱ��![]() ����ǰ�棻��
����ǰ�棻��![]() Ϊż��ʱ��
Ϊż��ʱ��![]() ����ǰ������Ҫ��������������������õ�һ���µ����У�
����ǰ������Ҫ��������������������õ�һ���µ����У�![]() ������������е�ǰ
������������е�ǰ![]() ���
���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ![]() ��
��
��2��������ʽ![]() ��
��![]() �����,��m��ȡֵ��Χ.
�����,��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
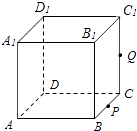
����Ŀ����ͼ��������ABCD��A1B1C1D1���ⳤΪ1��PΪBC���е㣬QΪ�߶�CC1�ϵĶ��㣬����A��P��Q��ƽ��ظ����������õĽ����ΪS��������������ȷ������д��������ȷ����ı�ţ���
�ٵ�0��CQ�� ![]() ʱ��SΪ�ı���
ʱ��SΪ�ı���
�ڵ�CQ= ![]() ʱ��SΪ��������
ʱ��SΪ��������
�۵�CQ= ![]() ʱ��S��C1D1�Ľ���R����C1R=
ʱ��S��C1D1�Ľ���R����C1R= ![]()
�ܵ� ![]() ��CQ��1ʱ��SΪ������
��CQ��1ʱ��SΪ������
�ݵ�CQ=1ʱ��S�����Ϊ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ��![]() ��ƽ��
��ƽ��![]() ���������ĸ������У���ȷ���ǣ� ��
���������ĸ������У���ȷ���ǣ� ��
A. ��m������n��������m��nB. ��m����n����m������l��������������
C. ����������m������m����D. ����������m������m������m����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com