练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在正方体ABCD﹣A1B1C1D1中，E，F分别为AB，BC中点，则异面直线EF与AB1所成角的余弦值为（ ）
    A.
    B.
    C.
    D.

    【答案】A
    【解析】解：如图，将EF平移到AC，连结B1C， 则∠B1AC为异面直线AB1与EF所成的角，
    ∵三角形B1AC为等边三角形，
    ∴故异面直线AB1与EF所成的角60°，
    ∴cos∠B1AC= ．
    故选A．
    【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】过点作一直线与抛物线交于两点，点是抛物线上到直线： 的距离最小的点，直线与直线交于点.

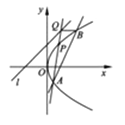
    (Ⅰ)求点的坐标；

    (Ⅱ)求证：直线平行于抛物线的对称轴.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若二次函数f（x）=ax2+bx+c（a，b，c∈R）满足f（x+1）﹣f（x）=4x+1，且f（0）=3．
    （1）求f（x）的解析式；
    （2）设g（x）=f（2x），求g（x）在[﹣3，0]的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A{x| ≥0}，B={x|x2﹣2x﹣3＜0}，C={x|x2﹣（2a+1）x+a（a+1）＜0}．
    （1）求集合A，B及A∪B；
    （2）若C（A∩B），求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面四个函数：（1）y=1﹣x；（2）y=2x﹣1；（3）y=x2﹣1；（4）y= ，其中定义域与值域相同的函数有（ ）
    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，在区间（﹣∞，0）上是增函数的是（ ）
    A.
    B.y=|x﹣1|
    C.y=x2﹣4x+8
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C与x轴相切，圆心C在射线3x﹣y=0（x＞0）上，直线x﹣y=0被圆C截得的弦长为2
    （1）求圆C标准方程；
    （2）若点Q在直线l1：x+y+1=0上，经过点Q直线l2与圆C相切于p点，求|QP|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）=logax，g（x）=loga（2x+t﹣2）2 ， （a＞0，a≠1，t∈R）．
    （1）当t=4，x∈[1，2]时F（x）=g（x）﹣f（x）有最小值为2，求a的值；
    （2）当0＜a＜1，x∈[1，2]时，有f（x）≥g（x）恒成立，求实数t的取值范围．
    （备注：函数y=x+ 在区间（0，1）上单调递减，在区间（1，+∞）上单调递增）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的不等式ax2+2x+b＞0（a≠0）的解集为 ，且a＞b，则 的最小值是 ．

    查看答案和解析>>

    同步练习册答案