
分析 (1)由过椭圆C的右焦点$F(\sqrt{2},0)$且经过短轴端点的直线的倾斜角为$\frac{π}{4}$,求出a,b,由此能求出椭圆C的方程.
(2)设点A,B的坐标分别为(t,2),(x0,y0),由OA⊥OB知tx0+2y0=0,再由${{x}_{0}}^{2}+2{{y}_{0}}^{2}$=4,利用基本不等式能求出线段AB长度的最小值.
解答 解:(1)设椭圆的短轴端点为(0,-b)(若为上端点则倾斜角为钝角),
则过右焦点与短轴端点的直线的斜率k=$\frac{0-(-b)}{\sqrt{2}-1}$=tan$\frac{π}{4}$=1,
∴$b=\sqrt{2}$,又$c=\sqrt{2}$,∴a=2,
∴C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.…(4分)
(2)设点A,B的坐标分别为(t,2),(x0,y0),其中x0≠0,
∵OA⊥OB,∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即就是tx0+2y0=0,…(6分)
解得t=-$\frac{{y}_{0}}{{x}_{0}}$.又${{x}_{0}}^{2}+2{{y}_{0}}^{2}$=4,
∴|AB|=(x0-t)2+(y0-2)2=(${x}_{0}+\frac{2{y}_{0}}{{x}_{0}}$)2+(y0-2)2=$\frac{{{x}_{0}}^{2}}{2}+\frac{8}{{{x}_{0}}^{2}}$+4(0<x0≤4),…(10分)
∵$\frac{{{x}_{0}}^{2}}{2}+\frac{8}{{{x}_{0}}^{2}}$≥4,(0<x0≤4),
且当$\frac{{{x}_{0}}^{2}}{2}=\frac{8}{{{x}_{0}}^{2}}$,即${{x}_{0}}^{2}$=4时等号成立,
所以线段AB长度的最小值为4.…(12分)
点评 本题考查椭圆性质、直线斜率、向量、基本不等式等基础知识,考查考查推理论证能力、数据处理能力、运算求解能力,考查函数与方程思想、化归与转化思想,考查创新意识、应用意识,属于中档题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
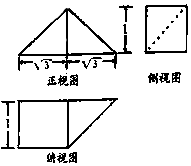 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )| A. | $4+3\sqrt{3}$ | B. | $3+3\sqrt{3}$ | C. | $4+2\sqrt{3}$ | D. | $3+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4R2=a3+b3+c3 | B. | 8R2=a2+b2+c2 | C. | 8R3=a3+b3+c3 | D. | 4R2=a2+b2+c2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a2+b2≠0,则a,b都不为零 | B. | 若a2+b2≠0,则a,b不都为零 | ||
| C. | 若a,b都不为零,则a2+b2≠0 | D. | 若a,b不都为零,则a2+b2≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2-$\sqrt{3}$ | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,$\frac{x-2}{x}$<0 | B. | ?x>0,$\frac{x-2}{x}$<0 | C. | ?x>0,0≤x<2 | D. | ?x>0,0<x<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com