
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据指数函数,复合函数,对勾函数的图象和性质,分析命题p1,p2的真假,进而根据复合命题,真假判断的真值表,得到答案.
解答 解:函数y=ex在R为增函数,函数y=e-x在R为减函数,
故函数y=ex-e-x在R为增函数,
即命题p1为真命题,
令t=ex,由x∈(0,1)得:t∈(1,e),
y=ex+e-x=t+$\frac{1}{t}$,
由对勾函数的图象和性质得:y=t+$\frac{1}{t}$,t∈(1,e)为增函数,
t=ex,也为增函数,
故y=ex+e-x,x∈(0,1)为增函数,
故命题p2为假命题,
故命题p1∧p2为假命题;
p1∨p2为真命题;
p1∧¬p2为真命题;
¬p1∨p2为假命题,
故选:B
点评 本题以命题的真假判断与应用为载体,考查了复合命题,指数函数,复合函数,对勾函数的图象和性质,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{63}}}{8}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 4 | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α、β相交但不垂直 | B. | α⊥β | C. | α∥β | D. | 以上均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
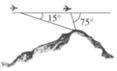 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com