
分析 (1)先求出函数的对称轴,得到函数的单调性,从而求出函数的最大值和最小值即可;
(2)先求出g(x)的解析式,求出函数的对称轴,根据函数的单调性得到关于m的不等式,解出即可.
解答 解 (1)∵f(x)=-x2+2x+2=-(x-1)2+3,x∈[0,3],对称轴x=1,开口向下,
∴f(x)的最大值是f(1)=3,又f(0)=2,f(3)=-1,
所以f(x)在区间[0,3]上的最大值是3,最小值是-1.
(2)∵g(x)=f(x)-mx=-x2+(2-m)x+2,
函数的对称轴是$x=\frac{2-m}{2}$,开口向下,
又g(x)=f(x)-mx在[2,4]上是单调函数
∴$x=\frac{2-m}{2}$≤2或$x=\frac{2-m}{2}$≥4,即m≥-2或m≤-6.
故m的取值范围是m≥-2或m≤-6.
点评 本题考查了二次函数的性质,考查函数的单调性、最值问题,是一道基础题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
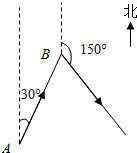 如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?
如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y(件) | 50 | 60 | 70 | 80 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com