
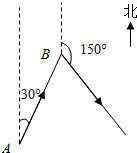
 如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?
如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短? 分析 设x小时后甲船到达C点,乙船到达D点,则BC=100-50x,BD=30x,由已知可得∠CBD=60°.由余弦定理得CD2=BC2+BD2-2BC•BD•cos∠CBD,即可得出结论.
解答 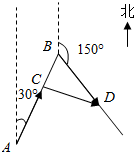 解:如图,设x小时后甲船到达C点,乙船到达D点,
解:如图,设x小时后甲船到达C点,乙船到达D点,
则BC=100-50x,BD=30x,由已知可得∠CBD=60°.
由余弦定理得CD2=BC2+BD2-2BC•BD•cos∠CBD,
即CD2=(100-50x)2+(30x)2-2(100-50x)•30x•cos60°
=100(49x2-130x+100),
当x=$\frac{130}{2×49}$=$\frac{65}{49}$时CD2最小,即CD最小
所以航行$\frac{65}{49}$小时两船之间距离最短.
点评 本题考查利用数学知识解决实际问题,考查余弦定理的运用,考查学生分析解决问题的能力,正确运用余弦定理是关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 0 | C. | 16 | D. | -$\frac{17}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10250 | B. | 3430 | C. | 825 | D. | 405 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com